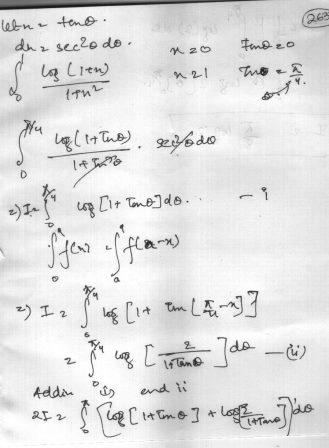
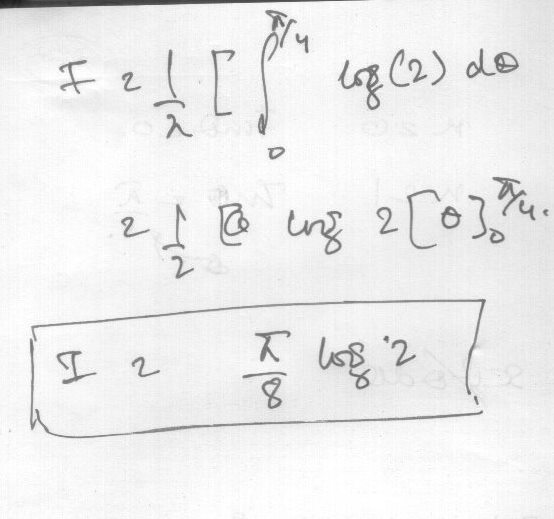
 Tanmoy Das What is the line after equation 1????Upvote·0· Reply ·2014-06-09 05:57:24
Tanmoy Das What is the line after equation 1????Upvote·0· Reply ·2014-06-09 05:57:24 Sahil Jain X= tany
Sahil Jain X= tany
\int_{0}^{1}\frac{\log_{e}(1+x)}{1+x^2}
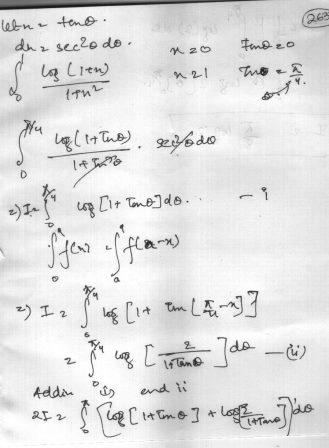
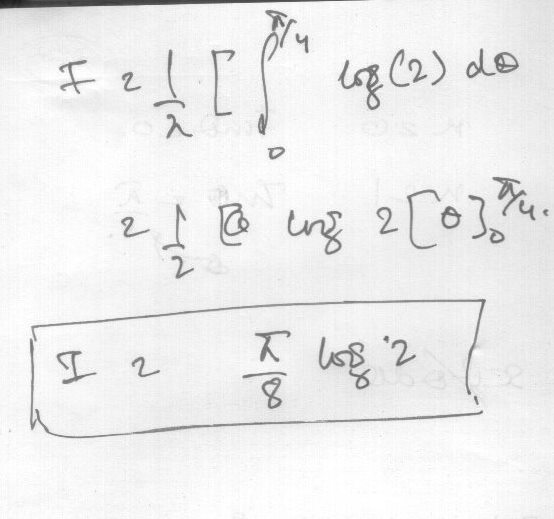
\hspace{-20}$Given $\bf{I = \int_{0}^{1}\frac{\ln(1+x)}{1+x^2}dx}$\\\\\\ Put $\bf{x=\frac{1-y}{1+y}=-\left(\frac{y-1}{y+1}\right)=-\left(\frac{y+1-2}{y+1}\right)}$\\\\\\ So $\bf{y = -1+\left(\frac{2}{y+1}\right)\;\;,}$ and $\bf{dx = -\frac{2}{(y+1)^2}dy}$\\\\\\ and Changing Limit .......\\\\\\ So $\displaystyle \bf{I = -\int_{1}^{0}\ln\left(\frac{2}{1+y}\right)\cdot \frac{1}{2(1+y^2)}\cdot \frac{-2}{(1+y)^2}\cdot (1+y)^2dy}$\\\\\\ Now Using the formula....$\bf{\int_{a}^{b}f(x)dx = -\int_{b}^{a}f(x)dx}$\\\\\\ So $\bf{\displaystyle I = \int_{0}^{1}\frac{\ln(2)-\ln(1+y)}{1+y^2}dy}$\\\\\\ So $\bf{I = \ln(2)\int_{0}^{1}\frac{1}{1+y^2}dy-\int_{0}^{1}\frac{\ln(1+y)}{1+y^2}dy}$\\\\\\ Now using the formula.... $\bf{\int_{a}^{b}f(x)dx = \int_{a}^{b}f(y)dy}$\\\\\\ So $\bf{I = \ln(2)\cdot \frac{\pi}{4}-I\Rightarrow I = \frac{\pi}{8}\cdot \ln(2)}$