1mv2 / 2 + kx2 / 2 = constant
differentiating. we should get.it. it'll be of the std form . get ω then substitute in T=2π/ω
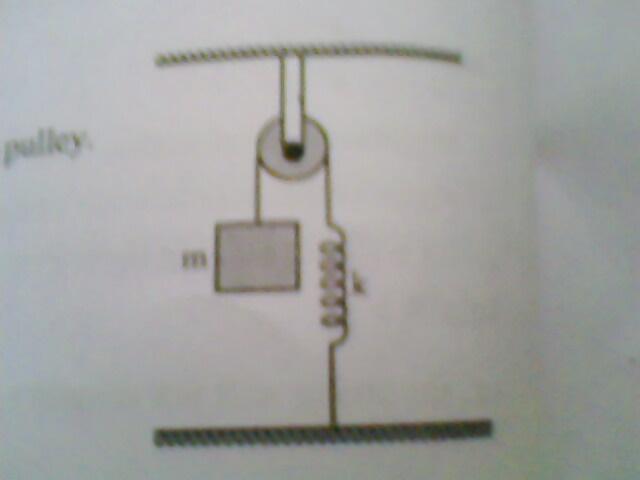Find the time period of oscillation of the pulley in the system shown. The moment of inertia of the pulley about its axis is I & the string does not slip over the pulley. The string & the springs are light.
Pls give the answer in detail....
b'caues I am still in initial stage of SHM
-
UP 0 DOWN 0 0 8
8 Answers
1
62let the displacement of the mass in the downward direction from its mean position be x
energy will be given by
ωr = v
1/2 mv2 - mgx + 1/2 I ω2 +1/2 k (x+x0)2
where kx0 = mg!
we have the equation.. you need to eliminate v and take the derivative..
try this.. if u cant complete .. do let me know.. i will put the final touches as well :)
Btw i dont like giving full answers cos i think it does inhibit the thinking capacity of students :)
(telling this to u cos am solving for the first time for u)
62no srinath u have to take into consideration potential energy and the rotational kinetic energry
62it is a simple topic... dont miss it..
it is all aobut writing energies properly :)
1which method is best ? force ,energy or torque ?
I feel comfortable with energy , can it be applied in all situations without cuasing problems.?
I've sometimes failde to complete problems bcoz of it. sometimes force is easier .but I prefer. energy , is this ok .?
62yes.. energy is generally the easier method..
but it depends on the qestions...
even i prefer energy at times :)
33i like force method actually i enjoy it although it becomes tricky at times and often energy method is much simpler......
Force method give every details but energy method is a powerful tool so need to be controlled as some form of energy is often left and it gives final results...
