1You are absolutely right
What is the probability of a chord in a circle to be of length less than D/2 where D is the diameter?
-
UP 0 DOWN 0 0 11
11 Answers
1This can be explained :-
You take any Diameter AB. On that diameter AB, when u draw any chord which is perpedicular to AB, then the length of chord increase from 0 to D & then again decrease to 0
(when you moves along AB from left ot right or right to left)
contd...
1contd...
So on AB we have two points ( one on left side of center & other on right side of center )...where we have limiting length of the chord .. i.e. (D/2)
So the probability will be:
(the length enclosed between these two points) divided by (length of AB)
You can see it comes out to be √3 / 2
1Nice Explaination ... [1]
I got the solution.
Let r be the radious of circle.
Those two points comes out to be equidistance from center.
The distance between center of circle to those points will be:
√ r2 - (0.5*r)2 = √3/2 r
The length enclosed between those two points comes out to be:
2* √3/2 r = √3 r
So the probability = √3r / 2r = √3/2
Please correct me if I am wrong.
33Is it given to find length less than or greater than D/2...
Is this not for length greater than D/2
62Well this is a very famous Paradox.
There are 3 answers possible and all 3 are right. I did not want to confuse you cos some/ most of you will nto understand the reason why we get three different answers and it still does not prove that they are equal.
try one thing: take chords originating from the same point!
Well this is called teh Bertrand's Paradox if any of you is interested in reading more.
May be I will put up this as the question of the day today!
33Earlier Nishant Bhaiya posted an additional q on this.....which got deleted..
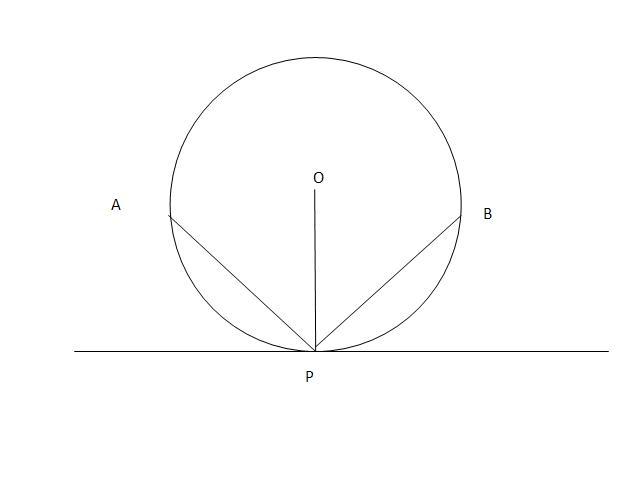
Why this is not 1200/1800
as any chord b/w PA and PB will be of length greater than R....
9no nishant sir there cant be 3 diff ans
only 1 ans is right as i ve explaine in QOD
62Celestine you are trying to disprove something that had been explained around 150 yrs back ;)
I saw your proof.. you tried a good one.. but there is a flaw in ur proof!