Combinatorics marathon
Inspired from artofproblemsolving we are gonna start a combithread maybe some questions will go above iitjee but i would like everyone to participate
Rules
1) u need to post solution to the question unsolved
2) for alternative solutions pls post it before question is solved
3) if not then pls message me the solution i will collect it (and most probably make a pdf out of it)
4) if u solve it ,preferabbly post a new question
5) Questions should be of the level of medium and above jee levels
6) (will plan to start of calculus too )
JEE question Genearlistation
THere are m boxes of m seperate color and corresponding m balls of same color .(each box can hold max one ball.) Find the number of ways of distributing balls such that NO BALL is in the box of its own color.
Hint start first when m=4,m=5 (o induction but will give u enough help)
21It's possible to find f in closed form from the recurrence relation u have mentioned and this involves elementary techniques like telescoping sum and product.
one can find D(n) by Principle of inclusion and exclusion as well(that's just how we calculate overlapping sets. )
262for a n*n matrix , (n-1)*(n-1) numbers can be filled randomly hence no. of ways = n(n-1)2
next if n is even ,
then each of the rest can be filled in n/2 ways so as to make the sum even.
hence total ways = n/2 * n(n-1)2
for n being odd,
rest can each be filled in (n-1)/2 ways
hence total ways = (n-1)/2 * n(n-1)2
1do this:
find the number of n by n matrices filled with numbers from 1-n (any repeated/omitted any number of times) such that the sum of every row and column is even
1total number of squares is
\sum_{k=1}^{9}{(10-k)^2(k)} ???
21It's not getting complicated.
see if our square is formed by k points, we have (k-2) squares inside it ..:)
1great ,never thought of that though ,problem is getting complicated ,nishant bhaiya help(hint)
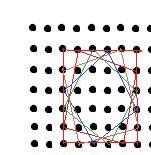
21no actually there are more squares.. this picture will surely give you a big hint...
what about the squares i have drawn ? you are only considering horizontal or vertical squares..
1@nasiko
answer to yoyr question is
12+22+32+...+102 ??
i think it is wrong as varun has said it belongs to olympiad level ,still ,my guess
21if i m awake this is just D(m)
Problem 2 Determine the number of squares with all their vertices belonging to the 10*10 by ten array of points defined in figure. (The points are evenly spaced) 
1as asked by varun
for the first question
let f(m) be a function denoting the number of possible ways of derangement
let the first box choose kth color ..this can be done in (m-1)ways
after this
there are two options with the kth box
1) it can choose the 1st box'color
In this case the sum reduces as f(m-2) ways
2)It does not chose 1st box's color
In this case the sum reduces as f(m-1) ways
so mathematically
f(m)=(m-1)(f(m-1)+f(m-2))
We know that
f(1)=0
f(2)=1
with this we can go on find for other integers
71Sorry, But these type of problems always embarrass me since I'm not able to solve them.
However, Keep up the good work!
21Alternative for you: (as u have the solution) In a regular 2n-gon the midpoints of all its sides and diagonals are marked.what is the maximum number of marked points that lie on a circle?
btw, i solved the q in my +1th and i don't think its too tough..it just needs a second thought and why do you find derangment 'hell'? please use such words that do not annoy others.
edits: aditya it's time for second thought.. there are more squares;)
262problem 2 :
no. of 10*10 squares = 1
" 9*9 " = 4
hence summing up we get total squares = sum of n2 (where n goes from 1 to 10)
or = n(n+1)(2n+1)/6 = 10*11*21/6 = 385
1what the hell is that ,are u referring to bernoullis theorem of putting all letters in wrong envelopes? could u give the proof thats the beauty isint it. and if u already read it somewhere let anyone else try
1@varun
he has solved the first question
he means D(m) is derangement function
1Source to above question
Titu anderseecus Path to combinatorics for undergraduates(Possibly too tough except for prophet sir to solve at 1st time i could do it 75% 1st time )
But 1st solve the 1st question and thne post new questions please