1decoder check it !!!,i don't think its correct!!!
find locus of center of circle which touches (y-1)2+x2=1 externally and also touches X axis.
if u're getting x2=4y and x=0,think again!!!
-
UP 0 DOWN 0 0 15
15 Answers
11I'm not sure whether this is correct or not!
If centre be (h,k), then we have
eqn of circle as
(x-h)^2+(y-k)^2=r^2.........(i)
From the fact that it touches given circle externally, we further have
h^2+(k-1)^2=(r+1)^2.......(ii)
From (i), we have 'r' in terms of h,k, as it touches x-axis!
Putting that in (ii), we can have the desired locus!
Pls correct me if wrong.
1357yes soumik, you are on the right track
just finish it off to get the answer.
1@ grandmaster,i am getting the same answer
my method:
let the circle be (x-h)^{2}+(y-k)^{2}=k^{2}
since it is touching the other circle externally therefore C1C2=r1r2
h^{2}+(k-1)^{2}=k^{2}
solving we get x2=2(y-1/2)
1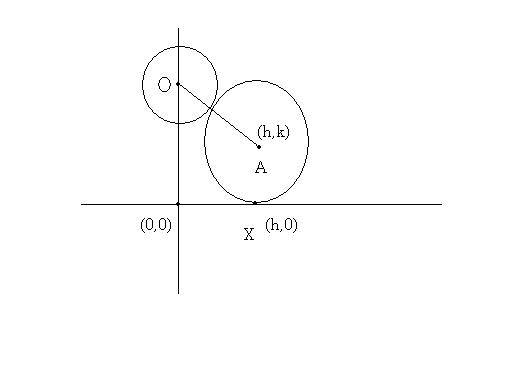
(y-1)2 + x2 = 1
Centre of the circle is (0,1).
Radius is 1.
Let the centre of reqd. circle be (h,k).
It touches the X-axis at (h,0) and its radius is k.
OA = k+1
again, OA2 = (k-1)2 + (h-0)2
Hence (k-1)2 + h2 = (k+1)2
or, h2 = 4k
Hence x2 = 4y is the reqd. locus
1357Hence (k-1)2 + h2 = (k+1)2
or, h2 - 2k2 =2
again check this step aveek
1357yes Aveek this is one of the answer you should get
But think is this the true locus?
what if y<0?
1yes thats where...manish bhaiya is ingeneous check below the x axis
3and aveek draw accurate rough diag bro ... see that circle with center 0,1 touches the x axis ...