6pls see ans
i hav other doubts.......
hey guys dese r my doubts
pls confirm
Questions-
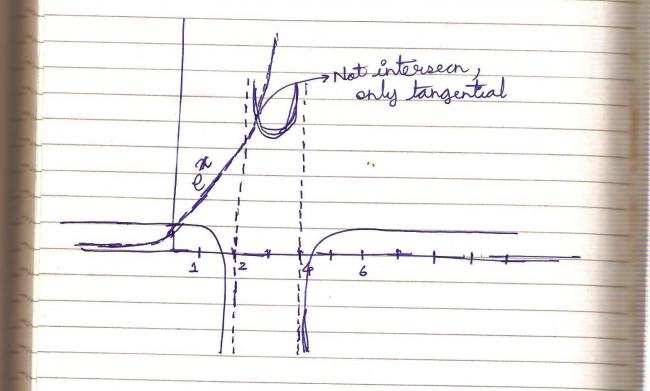
1.the no. of solns of the equn (x2-7x+6)/(x2-6x+8)=ex
(a)1
(b)2
(c)0
(d)4
my ans:d
2.If x!/y!=(12-y)!/(x2-23x+132)(10-x)!;x,y ε N,then wich one of the following may b true??
a.x=6
b.y=2
c.x+y=12
d.x+y=10
my ans b,c
3.If f(x)=x(2cos2(1/2x)-1) and the value of limx→∞f'(x)=k then (k+3) is equal to_______
this is intheger type q.
my ans 4
4.Let y=(x3+2x2x +2x +1)/(x2+x+1) then value of dy/dx at x=1 is _______
my ans 1
5.The minimum distance b/w the pts (mod sinx,0,0) and (- mod cosx,0,0) is ________-
my ans 1
(i din attempt dis one....:):P:( )
-
UP 0 DOWN 0 0 4
4 Answers
6hey pls sumbody check d ans.......................
39Q4. Make it an implicit function.
yx2 + yx + y = x3 + 2x2 + 2x + 1
We can make use of partial differentiation now.
Differentiate the function wrt x treating y as constant.
fx = 2xy +y + 0 - 3x2 - 4x -2 - 0
Similarly, differentiate the function wrt y treating x as constant.
fy = x2 + x + 1 - 0 - 0 - 0 - 0
Now by partial differentiation formula,
dydx = -fxfy
= 3x2+ 4x -2xy - y + 2x2 + x + 1
Very useful for implicit functions. I don't know if it could be used for nth derivative however...as mostly we get questions asking for d2ydx2.
So at x = 1,
dydx = 3 + 4 - 2(2) - 2 + 23 = 1.
:)
Q3. f(x) = x.cosx
f'(x) = cosx - xsinx
Is the limit undefined? I must be making a mistake there.
Q1. (x-1)(x-6)/(x-2)(x-4) = ex
Limx→∞(x-1)(x-6)/(x-2)(x-4) = 1 (Division of highest degree co-efficients)
So when x tends to infinity, curve's output is 1.
Also, we find the sign scheme of the polynomial by wavy curve method.
I think it has only one solution..