A long cylindrical conductor of radius 'a' has 2 cylindrical cavities of diameter 'a' through its entire length as shown in the cross section in the fig . a current 'I' is directed out of the page and is uniform throughout the cross section of the conductor .find the magnitude and direction of the magnetic field in terms of mu,I,a,r.
a)at point P1 (b)at point P2
how to do please help
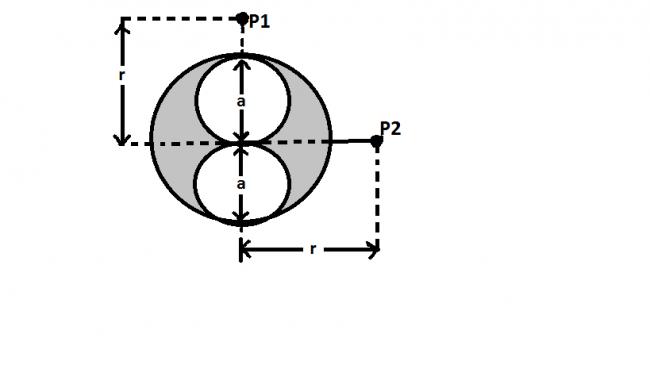
1\texttt{Let the current density be J} \\ \\ \mathrm{J=\frac{2I}{\pi a^2}}\\ \\
Now , consider this Cylinder
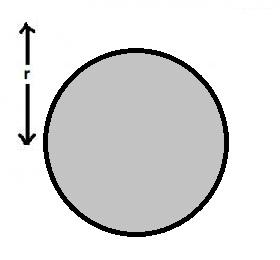
\texttt{Field at Point P1 due to this is } \\ \\ \mathrm{B_1=\frac{\mu_0 2I}{2\pi r}}
The direction is \mathrm{\hat{\theta}}
Now ,consider these two small cylinders one by one
But assume the current is going in the opposite direction
Due to the upper cylinder
\texttt{Field at Point P1 due to this is } \\ \\ \mathrm{B_2=\frac{\mu_0 I}{4\pi (r-\frac{a}{2})}}
Similarly ,consider the lower cylinder
\texttt{Field at Point P1 due to this is } \\ \\ \mathrm{B_3=\frac{\mu_0 2I}{4\pi (r+\frac{a}{2})}}
But B2 and B3 are in \mathrm{-\hat{\theta}}
So,net effet is
B1+B2+B3
B=\frac{\mu_0 I}{\pi}\left(\frac{1}{r}-\frac{1}{4}\left(\frac{1}{r-\frac{a}{2}}+\frac{1}{r+\frac{a}{2}} \right) \right)
Similarly , approach for 2nd one
1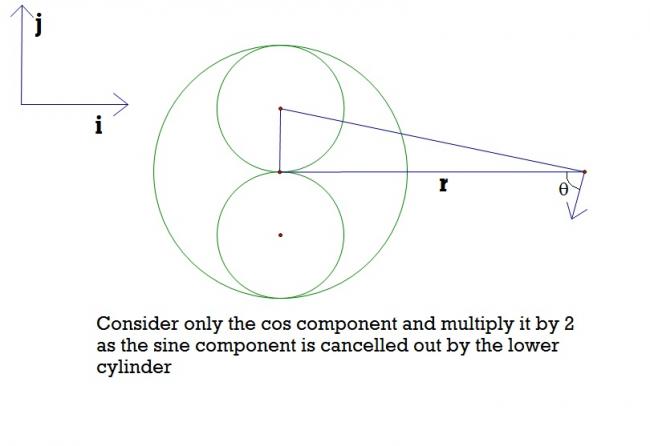
B=\frac{\mu_0 I}{4\pi\sqrt{r^2+\frac{a^2}{4}}}*\cos \theta \\ 2B=\frac{2 \mu_0 I}{4\pi\sqrt{r^2+\frac{a^2}{4}}}*\frac{a}{\sqrt{r^2+\frac{a^2}{4}}} (-\hat{i}) \\ \\ \\ 2B=\frac{2\mu_0Ia}{\pi\left(4r^2+a^2 \right)}(-\hat{i}) \\ \\ \texttt{B due yo biggest cylinder is } \\ \\ B'=\frac{\mu_0 I}{\pi r} (-\hat{j}) \\ \\ \bar{B}=B'-2B \\ \\ \bar{B}=\frac{\mu_0 I}{\pi}\left[\frac{2a}{4r^2+a^2}\hat{i}-\frac{1}{r}\hat{j} \right]
