1.Three particles are situated at 3 vertices of a triangle ABC of side a.Each particle moves with a speed v such that A moves towards B, B towards C and C towards A.Find the trajectory of the the particles.
66By symmetry, they must meet at the center (lets call it O). Suppose we look at the motion of A.
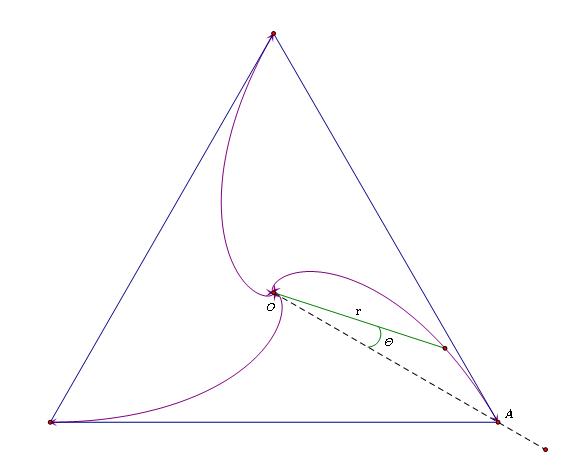
Taking OA as the initial line and the fact that OA = a√3, the distance r of the particle A from O at any angle θ, is given by the relation
r = a√3 e &ndash √3 θ
which gives the trajectory in the polar coordinate
1after asking my friend about this problem (an air 215 in jee 10)
he immediately recollected that it is from 200 PPP the first question
1Fact Is That The Solution To This Problem Gives An Interesting Result . A Curve Traced Out By A
Particle In Which The Radius Vector Forms A Constant Angle With The Tangent , Is Known As
LOGARITHMIC SPIRAL . This In Fact Was Discovered By Jacob Bernoulli In The Year 1693 . Its
General Equation Is given By -
r = a e b θ
Where " a " And " θ " Are As Shown By Kaymant Sir In His Diagram . The Factor " b " Is Given By ,
b = tan α ,
Whence , " α " = 60 o ------ In This Case .
So , b = √ 3 .
And " a " = a√ 3 ------ Again As Shown By Kaymant Sir .
So , The Trajectory Is -
r = a√ 3 e √ 3 θ
1- dadt = v - v cos 2 π3 ,
So , - dadt = 3 v2 , not √3 v2 .
But Here , r = a√3 .
So , - drdt = √ 3 v2 .
1v - v cos 2∩/3 gives v + v cos ∩/3 = answer of Sonne.
Ricky ... u r wrong!!!
1
-\frac{\mathrm{dr}}{\mathrm {dt}}=\frac{\sqrt {3}v}{2} \\ rd\theta\cos 60^0 =vdt \\ \\ \frac{\mathrm{d\theta}}{\mathrm {dt}}=\frac{2v}{r}
-\int_{\frac{a}{\sqrt{3}}}^{r}{dr}=\frac{\sqrt{3}v}{2}\int_{0}^{t}{dt} \\ \frac{a}{\sqrt{3}}-r=\frac{\sqrt{3}vt}{2} \\ r=\frac{2a-3vt}{2\sqrt{3}} \\ \\ d\theta=\frac{4\sqrt{3}vdt}{2a-3vt} \\ -\theta =\frac{4}{\sqrt{3}}\int_{0}^{t}\frac{d(-3vt)}{2a-3vt} \\ -\frac{\sqrt{3}}{4}\theta=\ln{\left( 1-\frac{3vt}{2a}\right)} \\ e^{-\frac{\sqrt{3}}{4}\theta}=1-\frac{2a-2\sqrt{3}r}{2a} \\
e^{-\frac{\sqrt{3}}{4}\theta}=1-\frac{2a-2\sqrt{3}r}{2a} \\ e^{-\frac{\sqrt{3}}{4}\theta}=\frac{\sqrt{3}r}{a} \\ \\ r=\frac{a}{\sqrt{3}}e^{-\frac{\sqrt{3}}{4}\theta}
damn it missed by a factor of 4 in exponent :( :( [17]!!
66We can take up a generalized case: A particle starting from a distance r0 from a fixed point (O in the following figure) moves with a constant speed v such that the velocity vector always forms an angle α (0<α<π/2) with the line joining the point O to the current location of the particle.
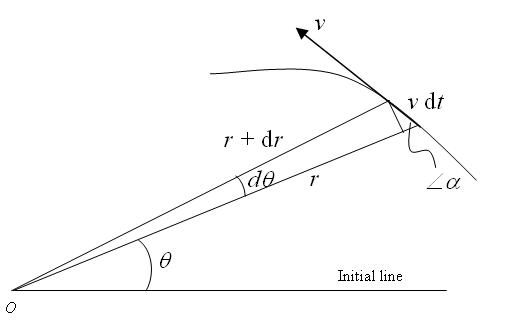
In a time dt, the particle moves an infinitesimal distance v dt. It's easy to see that
r dθ = v dt sin α ------- (1)
and
|dr| = v dt cos α
In our case, dr < 0, so that |dr| = - dr. Hence
&ndash dr = v dt cos α ------ (2)
Dividing (2) by (1), we get
&ndash dr r dθ =cot α
i.e. &ndash dr r =cot α dθ
Integrating and using the initial condition i.e. at θ=0, r = r0, we get
r = r0 e&ndash θ cot α
1oh i realise my mistake
-\frac{\mathrm{dr}}{\mathrm {dt}}=\frac{\sqrt {3}v}{2} \\ \frac{rd\theta}{\cos 60^0} =vdt \\ \\ \frac{\mathrm{d\theta}}{\mathrm {dt}}=\frac{v}{2r}
now we get
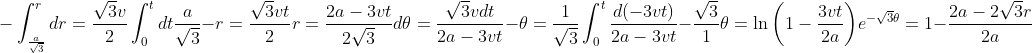
e^{-{\sqrt{3}}\theta}=1-\frac{2a-2\sqrt{3}r}{2a} \\ e^{-{\sqrt{3}}\theta}=\frac{\sqrt{3}r}{a} \\ \\ r=\frac{a}{\sqrt{3}}e^{-{\sqrt{3}}\theta}
sir is my prof right now
1is it neccesary to do this type of sums for preparing for jee.i mean radius vector type sums are not in jee syllabus.
is it neccesary to do irodov problems.
