33thats acc of block now draw FBD of block and find tension....
The figure shows one end of a string pulled down by a constant velocitty V.Assuming the pulleys to be massless and smooth,prove that the tension in string AB is mg(1+b2v2/4gx3)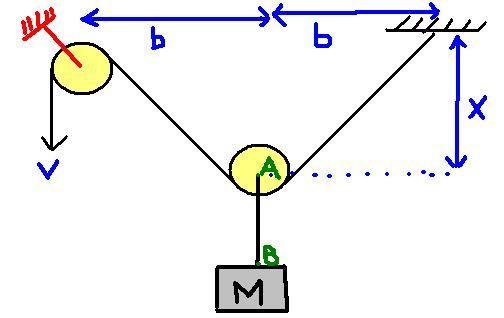
-
UP 0 DOWN 0 1 9
9 Answers
62let the length of string that hangs out be L
So,
L+2.√x2+b2 = c
dL/dt=v
Now we differentiate...
Then double differentiate to find accleration of point B
This will solve the question.
62Of course u need to write the FBD and pput that equation as well :)
11yes i solved with this...
L+2.√x2+b2 = c
dL/dt + 2/(√x2+b2).2x.(dx/dt) = 0
v=-4x/(√x2+b2).(dx/dt)
dx/dt = -√x2+b2 v / 4x
differentiating,
dv/dt = d/dt{4x/(√x2+b2)} . (dx/dt) + 4x/(√x2+b2). d2x/dt2
0 = d/dt{x/(√x2+b2)} . (dx/dt) + x/(√x2+b2). d2x/dt2
d/dt{x/(√x2+b2)} .√x2+b2 v / 4x = x/(√x2+b2). d2x/dt2
d/dt{x/(√x2+b2)} .(x2+b2) v = 4x2. d2x/dt2
4 d2x/dt2 = d/dt{x/(√x2+b2)} .{1+(b/x)2} v
d/dt{x/(√x2+b2)} = {1/√x2+b2 + x/(x2+b2)3/2 } . dx/dt
= -{1/√x2+b2 + x/(x2+b2)3/2 }.√x2+b2 (v / 4x)
= -{1 + x/(x2+b2) }(v / 4x)
Thus,
4 d2x/dt2 = d/dt{x/(√x2+b2)} .{1+(b/x)2} v
= -{1 + x/(x2+b2) }/ 4x . {1+(b/x)2}
I dont know what mistake i am making :(
62Dont have the patience to check the mistake..
L+2.√x2+b2 = c
dL/dt + 2/2(√x2+b2).2x.(dx/dt) = 0
v=-2x/(√x2+b2).(dx/dt)
dx/dt = -√x2+b2 v / 2x
dx/dt = -√1+(b/x)2 v/2
differentiating,
2/v d2x/dt2 = 1/(2√1+(b/x)2 ) {2b/x} {-1/x2} dx/dt
2/v d2x/dt2 = {-b/x3}/(√1+(b/x)2 ) dx/dt
2/v d2x/dt2 = {b/x3}.v/2
d2x/dt2 = {b/x3}.v2/4
3333I think tere some calculation mistake...
acc comes out to be :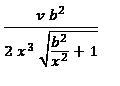
sorry theres v2b2 in numerator
now i think answer is coming....
T will be (1/2cosθ)(m*acc+mg)