Let C1 and C2 be the graphs of the function y = x2 and y = 2x, 0<x<1 respectively. Let C3 be the graph of a function y = f (x), 0<x<1, f(0) = 0. For a point P on C1, let the lines through P, parallel to the axes, meet C2 and C3 at Q and R respectively. If for every position of P (on C1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
1how how how did you know the very similar question gonna come in I.S.I????neways thanx for the question.:)
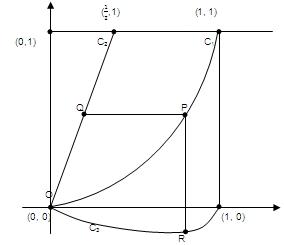
1let p be (t,t^2)
Area OPQ=\int_{0}^{t^2}{\sqrt{y}-\frac{y}{2}dy}
Area OPR=\int_{0}^{t}{x^2-f(x)dx}
these two areas are equal.
or \int_{0}^{t^2}{\sqrt{y}-\frac{y}{2}dy}=\int_{0}^{t}{x^2-f(x)dx}
Now differentiate both sides wrt t:
\left(t-\frac{t^2}{2} \right)2t=t^2-f(t)
or,f(t)=t^3-t^2
assumed that the function is cont in the int (0,1)
