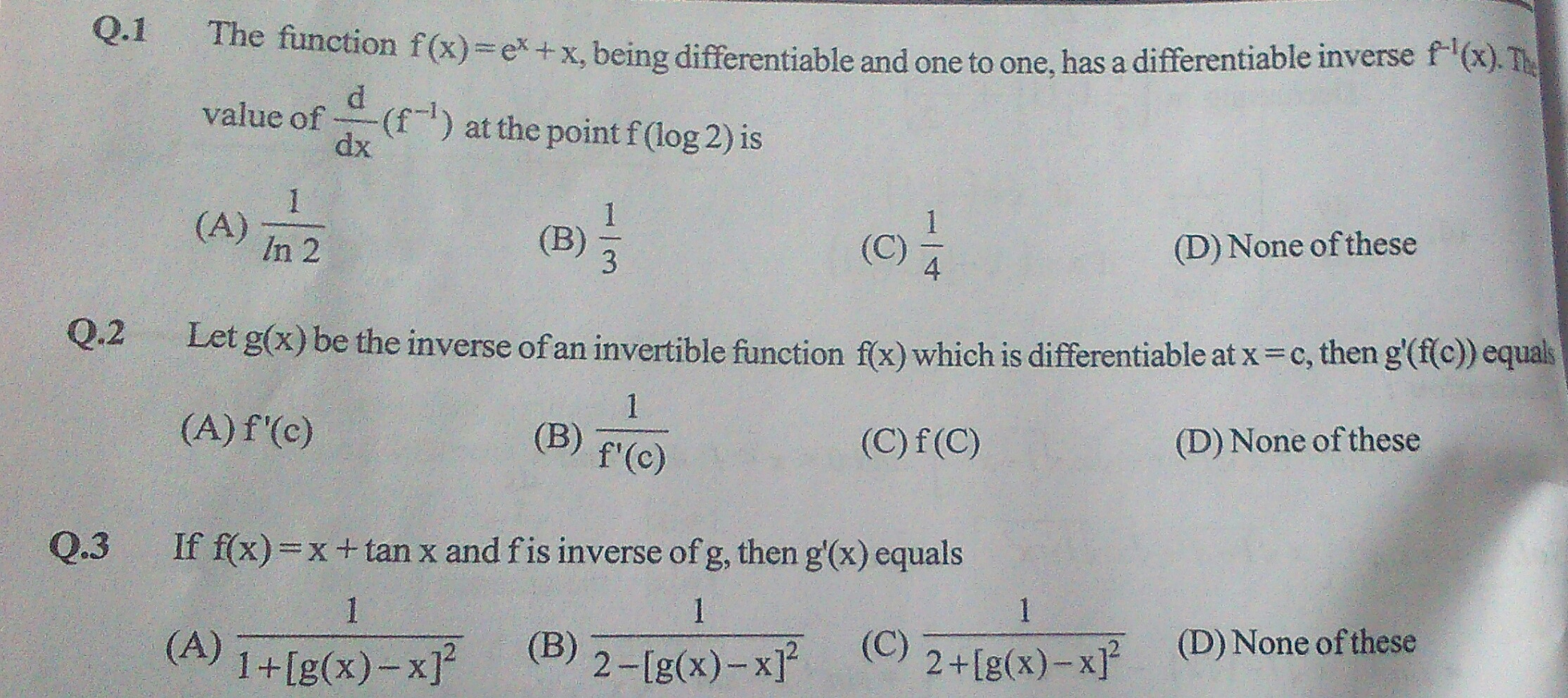differentiation

\hspace{-20}\bf{(3)\;\; } $ Given $\bf{f(x)=x+\tan x}$ and $\bf{f(x)}$ be the Inverse of $\bf{g(x)}$.\\\\\\ So If $\bf{g(x)}$ and $\bf{f(x)}$ are Inverse of each other, Then\\\\\\ $\bf{f(g(x))=g(f(x))=x}$, Now Diff. both side w. r.to $\bf{x}$\\\\\\ $\bf{f^{'}(g(x))\cdot g^{'}(x)=g^{'}(f(x))\cdot f^{'}(x)=1}$\\\\\\ So $\bf{f^{'}(g(x))\cdot g^{'}(x)=1..........................(1)}$ \\\\\\ and Given $\bf{f(x)=x+\tan x\;,}$ Now Diff. both side w. r. to $\bf{x\;,}$ we get\\\\\\ $\bf{f^{'}(x)=1+\sec^2 x = 1+1+\tan^2 x = 2+\left\{f(x)-x\right\}^2}$\\\\\\ Now Put $\bf{x=g(x)\;,}$ we get\\\\\\ $\bf{f^{'}(g(x))=2+\left\{f(g(x))-g(x)\right\}^2=2+\left\{x-g(x)\right\}^2}$\\\\\\ ( By using the formula $\bf{f(g(x))=x\;\;}$)\\\\\\ So Put value of $\bf{f(g(x))}$into equation.... $\bf{(1)\;,}$ we get\\\\\\ $\bf{g^{'}(x) = \frac{1}{f(g(x))} = \frac{1}{2+\left\{g(x)-x\right\}^2}}$\\\\\\ bcz $\bf{\left\{x-g(x)\right\}^2 = \left\{g(x)-x\right\}^2}$

\hspace{-16}\bf{(1)\;\; } $ Given $\bf{f(x)=e^x+x}$ and Let $\bf{g(x)}$ be the Inverse of $\bf{f(x)}$.\\\\\\ So we can write $\bf{g(x) = f^{-1}(x)}$. Now we have to calculate $\bf{\frac{d}{dx}(f^{-1}(f(ln 2)))=\frac{d}{dx}(g(f(\ln 2)))}$\\\\\\ Now $\bf{f(\ln 2) = e^{\ln 2}+\ln 2=2+\ln(2)}$\\\\\\ Now Using the formula if $\bf{f(x)}$ and $\bf{g(x)}$ are inverse of each other, Then\\\\\\ $\bf{f(g(x))=g(f(x))=x}$\\\\\\ $\bf{f^{'}(g(x))\cdot g^{'}(x)=g^{'}(f(x))\cdot f^{'}(x)=1}$\\\\\\ So $\bf{g^{'}(f(x))\cdot f^{'}(x)=1}$\\\\\\ Put $\bf{x=\ln (2)}$ and $\bf{f^{'}(\ln 2)=e^{\ln(2)}+1=2+1=3}$\\\\\\ We get $\bf{g^{'}(f(\ln 2))\cdot f^{'}(\ln 2)=1\Rightarrow g^{'}(f(\ln 2))=\frac{1}{3}}$