Polar Coordinates Mechanics

considering there is a fixed line(L-1) anywhere in space and from a fixed point O on this plane, there is a line which is moving in space(L-2)

considering a 3-d case

θ is the angle between L-1 and L-2

thus, for a fixed length of the moving line, there will be right circular conical sections on the sphere (centered at O) formed where the boundary of the base subtends same angle θ at the center with the axial line...

now that was the 3d approach.. if we consider any diametrical plane of the sphere, then our lives will become easy and also we would be later be able to generalise the case to 3-d

considering a horizontal plane that cuts the sphere and passes through point O and on which fixed line lies!

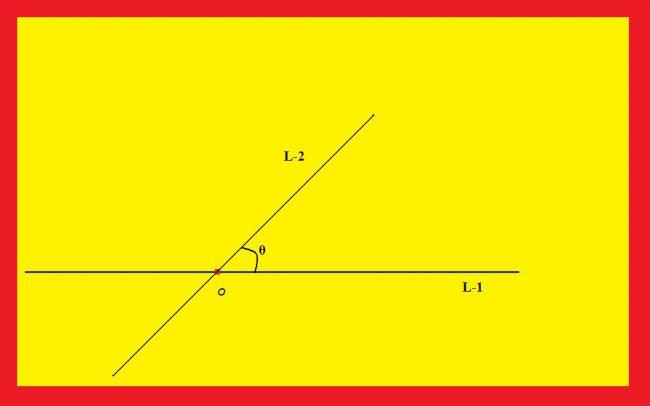
(i do not know why i ever gave this image :P)

again at θ=1rad R (which is distance from O) is becoming A
at θ=2 rad ; R=2A

also, this might be noted that R increases linearly with linearly increasing θ and is 0 at θ=0

again at θ=2π we see that the distance from centre has become 2πA

thus we might conclude that the particle is spiralling out from the centre! [1]

this much was the trajectory analytical part!

now it is said that the particle remains in contact wid both the walls during it's motion

i was initially confused to see the statement!

so i am providing the explanation for that statement!

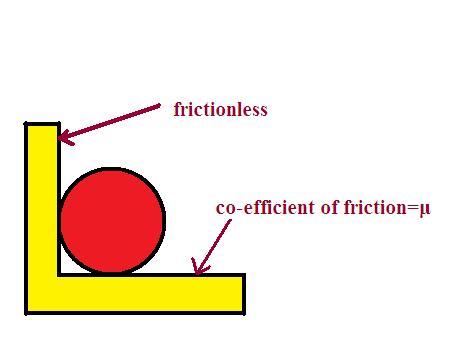
to keep the particle in spiralling trajectory,

it is guarded by a wall as in figure..

the vertical wall gives only normal reaction and not friction so only changes direction of the motion not magnitude of velocity...(W=Fxcos@ and here cos@=0 since @=90°)

so all the velocity decreasing force is applied by friction which acts in the opposite direction of motion always...

now look that the friction has nothing to do with changing the motion and also it is always opposite to direction of motion

again the normal reaction has no role in changing magnitude of the motion , it just changes the direction and so we can ignore everything and think the body is translating in a straight line and friction is trying to stop it!

same case here!

thus we will get velocity as a function of time easily!

v=v_o-at
and f=ma

do not get confused with the circular shape of the particle drawn in the above figure...(as nothing is mentioned in this problem, we can safely assume that there is pure translation and no rotation)
thus, we can safely assume, so far there is translation, friction is limiting i.e. f=μN and N=mg here

so f=μmg

and a=μg

thus v=v_o-μgt

now we have to find R as a func of time

I think this post has already become too long and anytime light chali jaa sakti hai so i ll add the post and continue writing in a new post :P

continuing from above post:

we can deduce from vector concept that there would be change in value of R only due to radial component of velocity!

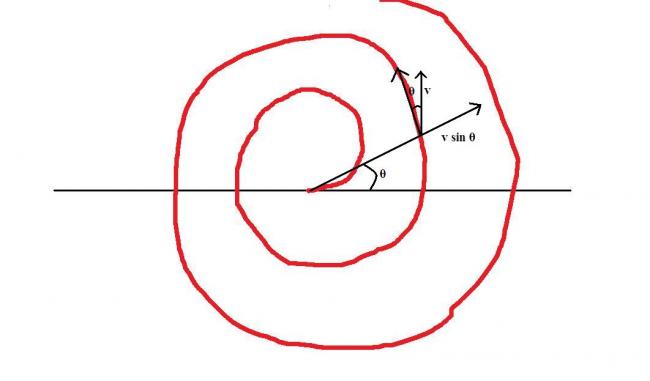
thus from figure, radial velocity's magnitude is v sin θ for polar angle θ of the particle...

let in time dt the particle proceeds radially by a distance dR

by given condition, dR=Adθ

so, dR=v_radial.dt
or, Adθ=vsinθdt
or, Adθ=(v_o-μgt)sinθdt
or, Adθsinθ=[v_o-μgt]dt
or, Acosecθdθ=[v_o-μgt]dt
or,\;\; \int_{0}^{\theta }{cosec\theta d\theta }=\int_{0}^{t}{\left[v_o-\mu gt \right]dt}
or,\;\; -\left[ ln \left( cosec\theta +cot\theta\right)-K\right]=v_ot-\mu g\frac{t^2}{2}
where,\;\; K=\lim_{\theta \rightarrow 0}\left(cosec\theta + cot\theta \right)
or,\;\; \left[ ln \left( \frac{cosec\theta +cot\theta}{K}\right)\right]=\frac{\mu gt^2}{2}-v_ot
or,\;\; cosec\theta +cot\theta=Ke^{\frac{\mu gt^2}{2}-v_ot}
or,\;\; tan\left(\frac{\pi }{4} - \frac{\theta }{2}\right)=Ke^{\frac{\mu gt^2}{2}-v_ot}
or,\;\; \frac{\pi }{4} - \frac{\theta }{2}=tan^{-1}\left[ Ke^{\frac{\mu gt^2}{2}-v_ot}\right]
or,\;\; \frac{\theta }{2}=\frac{\pi }{4} -tan^{-1}\left[ Ke^{\frac{\mu gt^2}{2}-v_ot}\right]
or,\;\; \theta =\frac{\pi }{2} -tan^{-1}\left[ Ke^{\frac{\mu gt^2}{2}-v_ot}\right]

thus,

\mathbf{{\color{red}\theta =\frac{\pi }{2} -tan^{-1}\left[ Ke^{\frac{\mu gt^2}{2}-v_ot}\right] }}
\mathbf{{\color{red}and\;\; R =A\left( \frac{\pi }{2} -tan^{-1}\left[ Ke^{\frac{\mu gt^2}{2}-v_ot}\right]\right) }}

sorry there was a mistake in the maths part...

**cosec\theta +cot\theta =K.e^{-v_ot+\mu gt^{2}/2}
or,\;\;sec\left(\frac{\pi }{2} -\theta\right) +tan\left(\frac{\pi }{2}- \theta\right) =K.e^{-v_ot+\mu gt^{2}/2}
or,\;\; tan\left[\left(\frac{\pi}{4} \right)+\frac{\left(\frac{\pi}{2}-{\theta} \right)}{2} \right] =K.e^{-v_ot+\mu gt^{2}/2}
or,\;\; tan\left[\frac{\pi}{2}-\frac{\theta}{2} \right] =K.e^{-v_ot+\mu gt^{2}/2}
or,\;\; cot\frac{\theta}{2} =K.e^{-v_ot+\mu gt^{2}/2}
or,\;\; {\color{red} \boldsymbol{{\theta} =2cot^{-1}K.e^{-v_ot+\mu gt^{2}/2}}}
{\color{red} \boldsymbol{and,\;\;R =2Acot^{-1}K.e^{-v_ot+\mu gt^{2}/2}}}

well which part of my signature?

as to dump physics is nearly impossible for me...

and as of not coming online much...that part is already in effect...my frequency of coming online has decreased tho the wavelength has remained constant [3]