Is d answer B??
A ball is rolling without slipping in a spherical shallow bowl as shown and executing SHM. If radius of the ball is doubled, the period of oscillation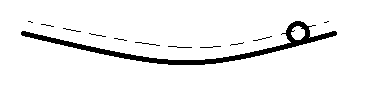
A) increases slightly
B) is reduced by a factor of 1/2
C) is increased by a factor of 2
D) decreases slightly
-
UP 0 DOWN 0 0 4

4 Answers
I don't think that the time period will change that much . The answer should be either A or D.
It's D since T=2Ï€√lg
On increasing the radius l decreases(Since l is the distance of the centre of ocillation and the COM of the ball).
However we can't say about the amount by which it will decrease since there is no information given regarding the point about which the oscillation is taking place and its distance from the COM of the ball.
 Soumyadeep Basu Yeah, it is given as D in the answer key. But can we use the expression of T for a simple pendulum in this case?Upvote·0· Reply ·2013-11-02 23:30:49
Soumyadeep Basu Yeah, it is given as D in the answer key. But can we use the expression of T for a simple pendulum in this case?Upvote·0· Reply ·2013-11-02 23:30:49 Shaswata Roy You can derive it if you feel like.The derivation is similar to the derivation for T for a simple pendulum.There is actually not much difference b/w the SHM for a simple pendulum and that in the above case(since in both the cases the sin component of g is causing the SHM).The only difference is that in one case the normal force is balancing the cos component of g while in the other the tension in the string is.
Shaswata Roy You can derive it if you feel like.The derivation is similar to the derivation for T for a simple pendulum.There is actually not much difference b/w the SHM for a simple pendulum and that in the above case(since in both the cases the sin component of g is causing the SHM).The only difference is that in one case the normal force is balancing the cos component of g while in the other the tension in the string is. Akash Anand I guess Shaswata is correct, and its a quite logical explanation. Good Work
Akash Anand I guess Shaswata is correct, and its a quite logical explanation. Good Work