Problem: When a photon is emitted from an atom, the atom recoils. The kinetic energy of recoil and the energy of the photon come from the difference in energies between the states involved in the transistion. Suppose, a hydrogen atom changes its state from n=3 to n=2. Hydrogen atom changes its fractional change in the wavelength of light emitted, due to recoil.
My solution:
Difference in energy in the transition from n = 3 to n = 2 is
E2 –E3 = 13.6 (1/22 –1/32) =1.89 ev.
Conservation of Energy:
1.89ev = Ephoton + K.Erecoiled atom --- (1)
Conservation of Momentum:
Momentum of system before the emission was zero. So,
0 = Pphoton + Patom
=> both has same momentum `p` just direction is opposite.
substituting in (1) eqn :
pc + p2/2m = 1.89ev
where `m` is the mass of the recoiled atom. Which is not known. This is where I'm stuck.
Answer given in HC Verma is 10-9.
I've H.C Verma Solutions book also. In that, this is the solution Given:
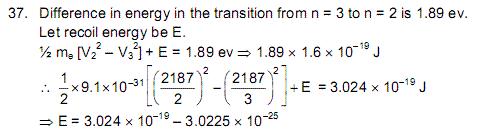
I cannot understand this solution either.
-
UP 1 DOWN 0 0 1

1 Answers
This question can be done by doing momentum and energy conservation.By this we will get a quadratic equation and by solving that equation and putting all the values we will get the fractional value of wavelength as 10^-9.