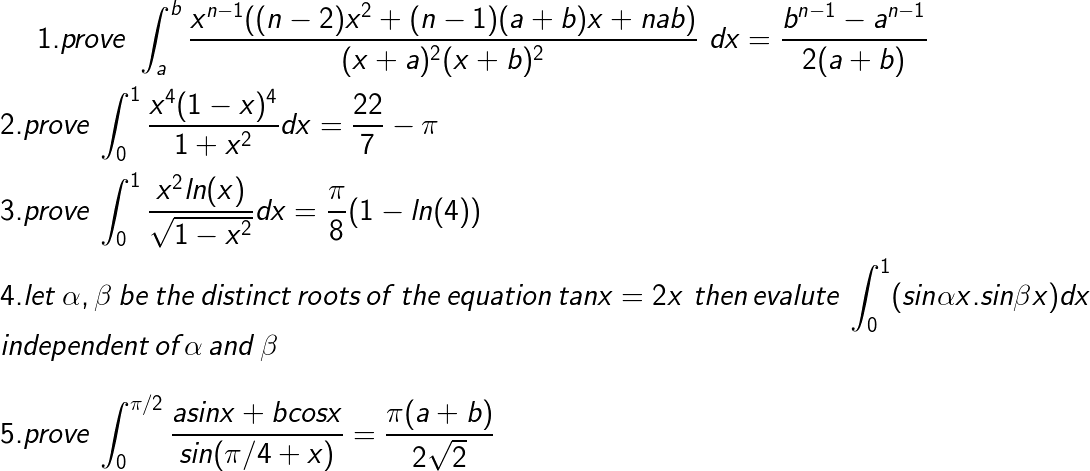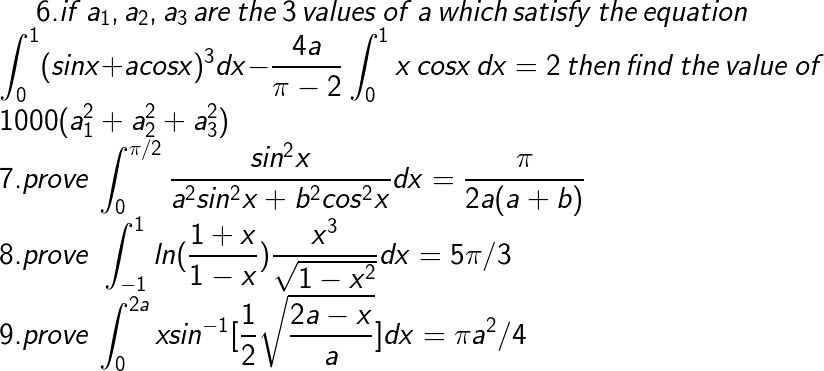146for the fourth q one of the roots will be zero which makes the whole integral expression zero which is independent of α and β
Swastik Haldar thanks.Upvote·0· Reply ·2014-08-06 09:23:30
6 Answers
146
1357second one is x8-4x7+6x6-4x5+x41+x2
divide it to simplify it
- Swastik Haldar sir what about the sixth one? I tried diffrentiating with respect to a three times and then integrating, but it's not working.
146for q 5 sin[Ï€/2-(Ï€/4+x)]=sin(Ï€/4+x)
now apply the rule of definite integral ∫baf(x)=∫abf(b+a-x) and also expand sin(x+π/4) by trigonometry. then after simplifying a bit you will see that numer. and denom. is getting cancelled then putting the limits you will get the result.
146for q 8 just apply the concept of integration by parts(LIATE rule) and there for the integration of x^3/√(1-x^2) take x=sinθ as substitution