1Please help
Find locus of point of intersection of tangents drawn at the end points of a variable chord of parabola y^2=4ax ,which subtend constant angle tan^-1 b at the vertex
-
UP 0 DOWN 0 1 7
7 Answers
62take teh points at at2, 2at
and am2, 2am
the angle between them has to be b
now try to find the same...
11What we know is that point of intersection of tangents at (at2,2at) and (ak2, 2ak) is given by (atk, a{t+k})
From given conditions, we have
tanb = 2k-2ttk+4, from which tk comes out to be 2(k-t)tanb
Thus x=2a(k-t)tanb, y=a(t+k)
Solve these 2 for t,k in terms of x,y and put them in 1 of the equaions to get locus....
66Refer to the diagram below: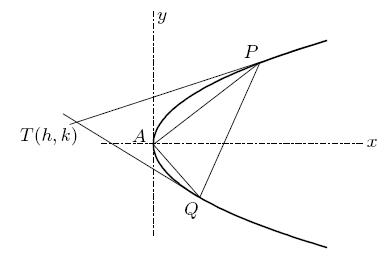
Let PQ be the variable chord, the tangent at whose extremities meet at T(h,k). Then, PQ is the chord of contact of the tangents drawn from T. As such the equation of PQ can be written as
ky = 2a(x+h) => ky - 2ax = 2ah ------------(1)
AP and AQ are the straight lines joining the points of itersection of the line (1) with the parabola y2 = 4ax. As such, we can obtain the equation representing AP and AQ by homogenizing the equation of the parabola using (1). So the combined equation of AP and AQ is
y2 = 4ax (ky - 2ax2ah)
which is same as
4ax2 - 2kxy + hy2 = 0
Since the angle between these pair of lines is tan-1 b, we get
tan(tan-1 b) = 2√k2 - 4ah4a+h
which gives, after simplification,
4(k2 - 4ah) = b2(h+4a)2
Since, this equation is satisfied by all positions of T(h,k), the locus of T becomes
4(y2 - 4ax) = b2(x+4a)2