11Ans : 3(√10 + 3)
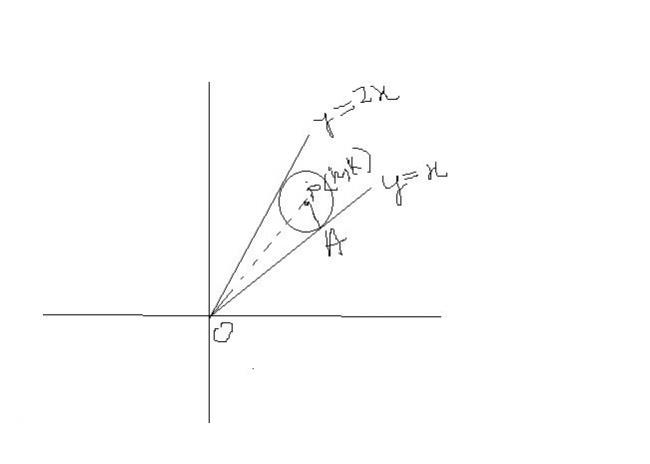
Let 2x2+y2-3xy=0 be the equation of a pair of tangents from origin O to a circle of radius 3 with center in the first quadrant. If A is one of the points of contact, Find the length OA
-
UP 0 DOWN 0 0 6
6 Answers
1k the esiest one :P
now |k-2h| =3√5 , |k-h|=3√2
solving this we get P.
then OA2=OP2-PA2
12x2+y2-3xy=0
i.e (y-x)(y-2x)=0
lines are y=x and y=2x
let C(a,b) be the center of the circle whose tangents are two lines y=x and y=2x
clearly b>a and b<2a
radius=3=length of perpendicular from C on the two tangents
=b-a/√2 = 2a-b/√5
from above, a=3(√5+√2) and b = 3(√5+2√2)
OA2=OC2- radius2
=(a2+b2-9
=9(7+2√10)+9(5+8+4√10)-9
=171+54√10=90+81+2√90x81=(√90+√81)2
therefroe OA=9+√90=9+3√10
11
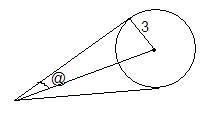
Angle b/w tngnts = 2@
tan 2@ = 2√9/4 - 2 /(3) = 1/3
So, tan @ = √10 - 3
Also tan @ = 3/oa
So,oa = 3/(√10 - 3) = 3(√10 + 3)
1let C(a,b) be the center of the circle whose tangents are two lines y=x and y=2xclearly b>a and b<2a
Plz explain this