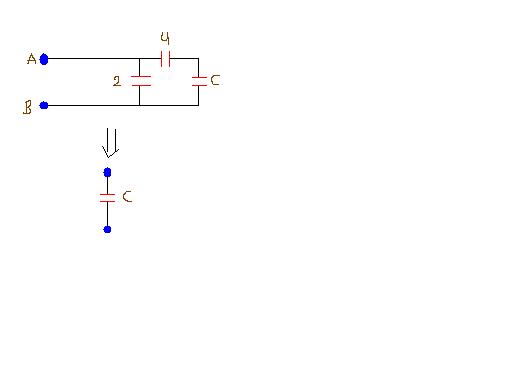
Let the equivalent capacitance b/w points A and B is given by C,
The equivalent capacitance of the ladder b/w A and B is independent of the no of sections in b/w ,
C = [(4 C) / (4+c)] + 2
Therfore C=4 uF
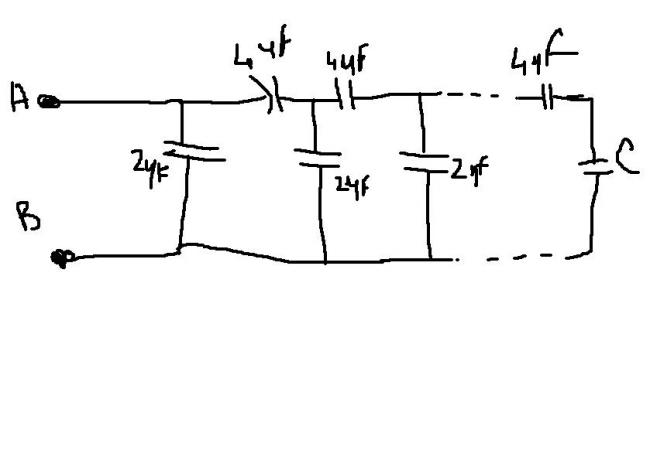
A finite ladder is constructed by connectiong several sections of 2uF and 4uF capacitors combination as shown.
IT is terminated y a Capacitor of C...wht should be the value oif C...so that the equivalent capacitence of the ladder betweeen A and B becomes independent of the sections in betweennnnn

Let the equivalent capacitance b/w points A and B is given by C,
The equivalent capacitance of the ladder b/w A and B is independent of the no of sections in b/w ,
C = [(4 C) / (4+c)] + 2
Therfore C=4 uF
@msp
Sice it is an INFINITE series, so ,there will be negligible change if the arrangement is done as shown in the figure.
ya i know dat tush.
where u have explained dat taking Ceq=C means dat that the equivalent capacitence of the ladder betweeen A and B becomes independent of the sections in betweennnnn
Since it is an INFINITE series, so the equivalent capacitance b/w A and B is independent of the no of sections.(As I told in the earlier post).
Now if the problem is twisted and at subsequent steps(strating from 2nd 4f capacitor) 4F is replaced by 2F,1F,1/2F,1/4F,1/8F respectively,means the value is halved at each step,then can u solve it.??
A finite ladder is constructed by connectiong ...so guys plz dun take it as a infinite ladder!!!!
THE UNKNOWN CAPACITOR SATISFYING THE GIVEN REQUIREMENTS IS (C)
.....the logic is to connect (C) across the terminal ends so that capacitance across the previous terminal also becomes (C)...this reduces the circuit to
thus , {(C+C2)C1}/ {C1+C+C2} = C
...THIS GIVES A QUADRATIC IN (C)...which gives (C) as one of its roots....
/////////////////done//////
 assuming that the c value dominates (n-1) combinations of capacitors and taking the equivalent capacitance as itself c then you can get the value of c
assuming that the c value dominates (n-1) combinations of capacitors and taking the equivalent capacitance as itself c then you can get the value of c
AS C=(4C/4+C) (as c is in series with 4f) +2f(as it is parallel with (4C/4+C)