4√5tan(theeta)..??????
A man throws a ball horizontally with a velocity vo from a distance of 4m vertically above the lowest point of the incline.He throws it towards the incline.The ball hits the inclined plane perpendicularly.Find vo?(g=10m/s2)
-
UP 0 DOWN 0 1 8

8 Answers
actually I forgot angle of incline is 30...
@anik....anyway your answer is wrong....
i know the answer...just wanted to know your approach as the way i did maybe long..
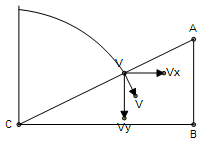
\dpi{150} \fn_cs \textit{Let the velocity at the point of collision be v}
\dpi{150} \fn_cs v_{x}=v_{0}\textit{ and }v_{y}=gt
\dpi{150} \fn_cs \frac{v_{x}}{v_{y}}=tan(30^{\circ})\Rightarrow v_{0}=\frac{gt}{\sqrt{3}}.....(i)
\dpi{150} \fn_cs \textit{Vertical height of point of collision above the ground = y}
\dpi{150} \fn_cs \textit{Horizontal distance of point of collision from starting point = x}
\dpi{150} \fn_cs x = v_{0}t
\dpi{150} \fn_cs \frac{y}{x}=tan(30^{\circ})\Rightarrow y=\frac{x}{\sqrt{3}}
\dpi{150} \fn_cs \frac{y}{x}=tan(30^{\circ})\Rightarrow y=\frac{x}{\sqrt{3}}=\frac{v_{0}t}{\sqrt{3}}=\frac{gt^{2}}{3}
\dpi{150} \fn_cs \textit{Vertical distance covered + Height of point of collision above ground = 4}
\dpi{150} \fn_cs \frac{1}{2}gt^{2}+\frac{1}{3}gt^{2} = 4\Rightarrow t = \frac{2\sqrt{3}}{5}
\dpi{150} \fn_cs \textit{Substituting this in (i) we get }v_{0}=4m/s