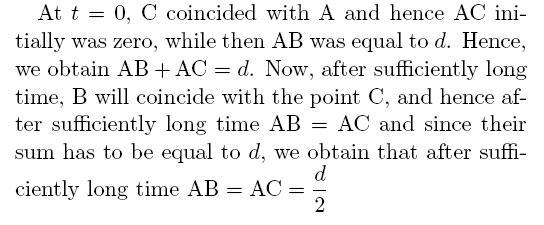How come vcosA - v = v(1 - cosA)??? In Vca?
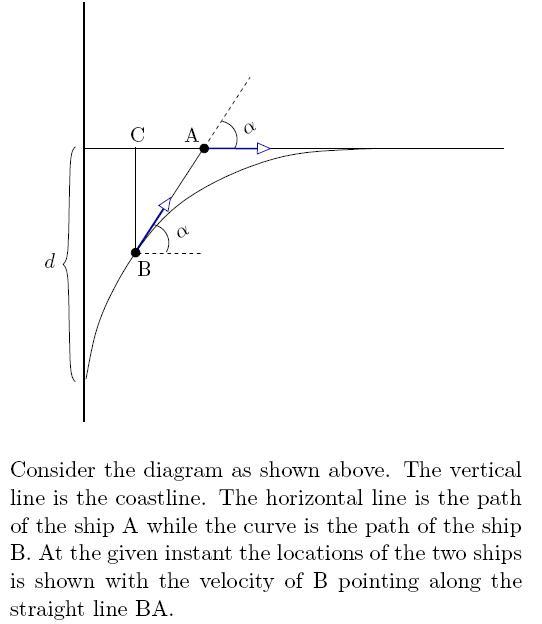
Q1. Two ships A and B originally at a distance d = 3 km from each other depart at the same time from a straight coastline. Ship A moves along a straight line perpendicular to the shore while ship B constantly heads for ship A, having at each moment the same speed as the later. After a suffciently large interval of time, ship B will obviously follow ship A at a certain distance. Find this distance.
A more generalised one...
Q2. Two particles A & B start from positions ( 0, 0 ) & ( 0, -d ) and move with constant speeds v & u respectively . A moves along x - axis and B moves such that its velocity is always aimed at A . Let r be the distance between them and be the angle made by the velocity of B with X - axis , at some time t .
Prove that , r/d = [(1-cos\theta )^u^/^v]/[(sin\theta )^u^/^v^+^1]
-
UP 0 DOWN 0 4 17

17 Answers
sir pehle to iska matlab bataoo......"""the concept of invariance.""'
the second one is even easier!
let the angle at any instant be θ to the horizontal
then we have
dr/dt=vcosθ-u
and
dθ/dt=-vsinθ/r
so dt=dr/vcosθ-u
(u-vcosθ)dθ/vsinθ=dr/r
integrating we get .
log(cosecθ-cotθ)u/v - logsinθ=log(r/d)
we get
r/d=(cosecθ-cotθ)u/v/(sinθ)
thus
r/d=(1-cosθ)u/v/(sinθ)(u/v)+1
Ship B sees that it is heading to A or ship A sees so or observer from ground see that...
I think ship B sees that...
the first one is not lengthy at all ..
we have if the line joining the two particles makes an angle θ with the horizontal ..
and if the distance between them is r
dr/dt=(ucosθ-u)
intial r=d final let D
w get
D-d=0∫tucosθdt -0∫tudt
further we have
final distance D also= ∫udt-∫ucosθdt
so we get D-d=-D
D=d/2 =1/5
ok sir........will try to do further.......[1][1]
vaise what are its chances of coming in JEE??
becoz it looks a bit lengthy.......
it tried to form a 3-4 eqn but nothing gained out of them[2][2]
anyways 2 things are clear........
dx/dt = u cosθ
and dy/dt = usinθ
what next????[12][12]
At time t is the situation like this??????
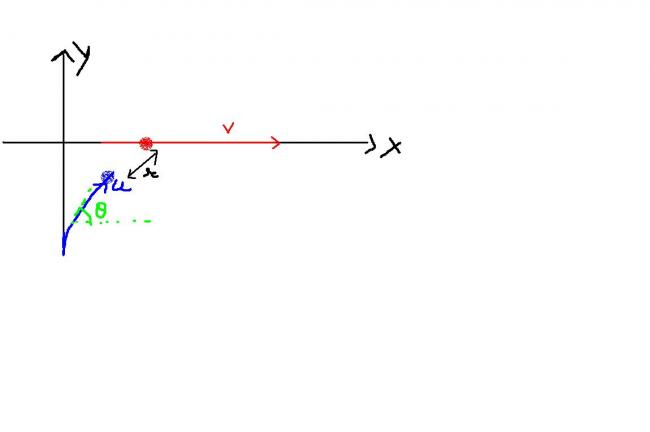
If yes then i will try to do it