30pls explain.
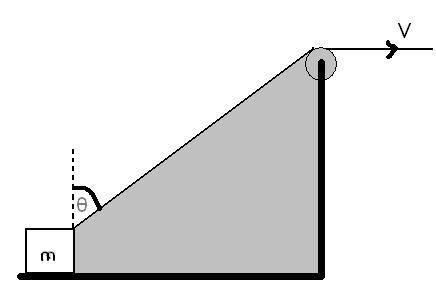
A block is dragged on a smooth plane with the help of a rope which moves with velocity v shown in Fig. The horizontal velocity of the block is
a)v
b) vsinθ
c) v/sinθ
d) v/cosθ
-
UP 0 DOWN 0 0 11
11 Answers
49
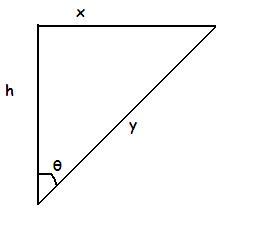
well from triangle we can say x=√y2-h2
so, dxdt=2y2√y2-h2.dydt
also dydt=v
so vx=v.(y√y2-h2)=v.yx=vsin θ
sin θ= yx
1can anyone tell me that how can we approach that it is a type of constraint relation.
i want to know the basic approach
49the basic approach is v=ds/dt wer s= displacement
and a=dv/dt
thus if we can some how relate the displacements of the particles we can relate their velocities and accelerations!! :)
1i easily explained yesterday to my friend yesterday that answer is v/sintheta but today after 22 hrs i forgot myself that how my answer came yesterday
1The component of block's velocity along the rope is equal to v.
v'sin(theta)=v (v' is velocity of block)
this is due to the fact that the string is unstretchable this can be proven by constaint relations or power method.