A particle is projected from a point to hit an apple as shown in the figure.The particle is directly aimed at the apple.Show that the particle will not hit the apple.Now show that if the string with which the apple is hung is cut at the time of firing the particle, then the particle will hit the apple. 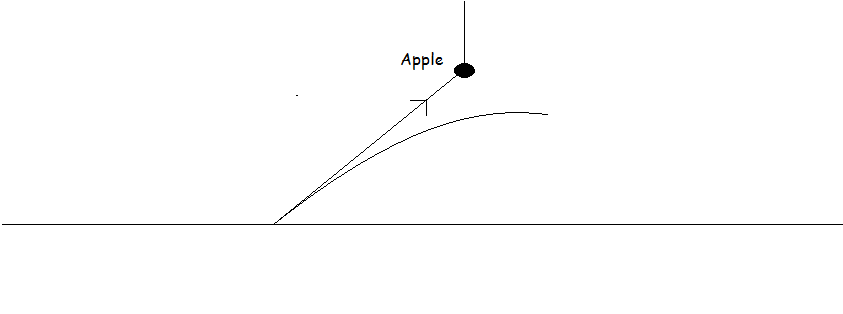
-
UP 0 DOWN 0 0 1

1 Answers
let the angle of projection be θ,velocity of projection be v,height of apple from be h and horizontal distance from the point of projection be x.
using the equation of trajectory
y=yo+xtanθ-gx22(vcosθ)2
putting yo=0,tanθ=h/x,cosθ=√x(x2+h2)
we get,
y=h-g(x2+h2)/2v2
y=h-(a positive quantity)
so at a distance the particle will be at a height less than h(the hieght of apple from the ground).
so the particle will never hit the apple.
now if the string with which the apple is hung is cut at the time of firing the particle, the apple will fall a distance of gt2/2 in time 't'.
so for the particle to hit the apple t=x(vcosθ).so the particle should be at a height of h-gx2(vcosθ)2
the above expression shows that the particle will hit the apple if it is projected with a particular velocity of projection for given value of 'h' and 'x'