a uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end .The tension in the rod at a distance x from the axis is?
2305
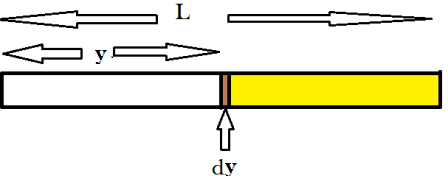
Consider an element of width dy and having mass dm.
Centripetal force acting on this element ,
d\mathcal{F}_c=\omega^2 y\,dm=\frac{M}{L}\omega^2y\,dy
Net centripetal force acting on the rod till length x ,
\mathcal{F}_{c,x}=\int\limits_0^x \frac{M}{L}\omega^2y\,dy=\frac{M\omega^2 x^2}{2L}
Net centripetal force acting on the whole rod ,
\mathcal{F}_{c,l}=\int\limits_0^l \frac{M}{L}\omega^2y\,dy=\frac{M\omega^2 L}{2}
\mathcal{F}_{c,x}+T=\mathcal{F}_{c,l}
T=\frac{1}{2}M\omega^2 L\left(1-\frac{x^2}{L^2}\right)
Sushovan Halder thanks a lot481Is the answer Mw^2L/2
Anurag Ghosh sry Mw^2x/2??Sushovan Halder i need the solution481Sry dude the answer must be M*w^2*x^2/2L....See assume a rod of lenght L which is hinged at 1 end.....its rotating with an angular velocity w......now take an element dy of mass dm at a distance y.......Now,
dm/dy=M/L -> dm=M*dy/L
Now...at d distance y,Tension=centrifugal force
So,dT=dm*w^2*y -> dT=M*w^2*y*dy/L
Integrating,we get.......T=M*w^2*x^2/2L.....
Sushovan Halder but the answer is Mw^2L(1-x^2/L^2)/2