1for any doubt ping me on 8802855324
A heavy, flexible, inelastic chain of length L is placed almost symmetrically onto a light pulley which can rotate about a fixed axle, as shown in the figure.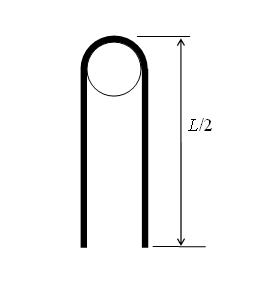
What will the speed of the chain be when it leaves the pulley?
-
UP 0 DOWN 0 9 31
31 Answers
66The futile search for the horizontal force (which you are looking for) would lead you nowhere, simply because it's not there (who will supply that horizontal force). However, therein lies a big hint: the center of mass cannot shift horizontally.
Now, can you guess what's happening?
@Nishant: The profile pic is that of Richard Feynman, one of the greatest teacher of this century, and one of the Nobel Award winner for Quantum Electrodynamics, one of the most precise theory constructed.
66Probably, people have forgotten this. Let me give the answer so at least you know what are you looking for.
Answer: The chain will leave contact with the pulley when a length \dfrac{L}{2\sqrt{2}} of the chain has gone to the other side and the speed at this instant is v=\dfrac{\sqrt{gL}}{2}.
66Of course, we can conserve energy as the friction won't do any work. However, as I have already said, the center of mass cannot shift horizontally. This does not mean we have to neglect the radius of the pulley or anything like that. In fact, this will imply (not very obviously) that the chain must loose contact when a part of it is still on the other side of the pulley. That is to say that when it leaves contact with the pulley a part of it is still moving up!!. However, we don't what part of the chain is still moving up. The point is that we should not be inclined to think that the chain is loosing contact, when one end of it is just touching the figure (like that shown by Priyam in #16). This a priori assumption is wrong.
33[2]
√3gl/4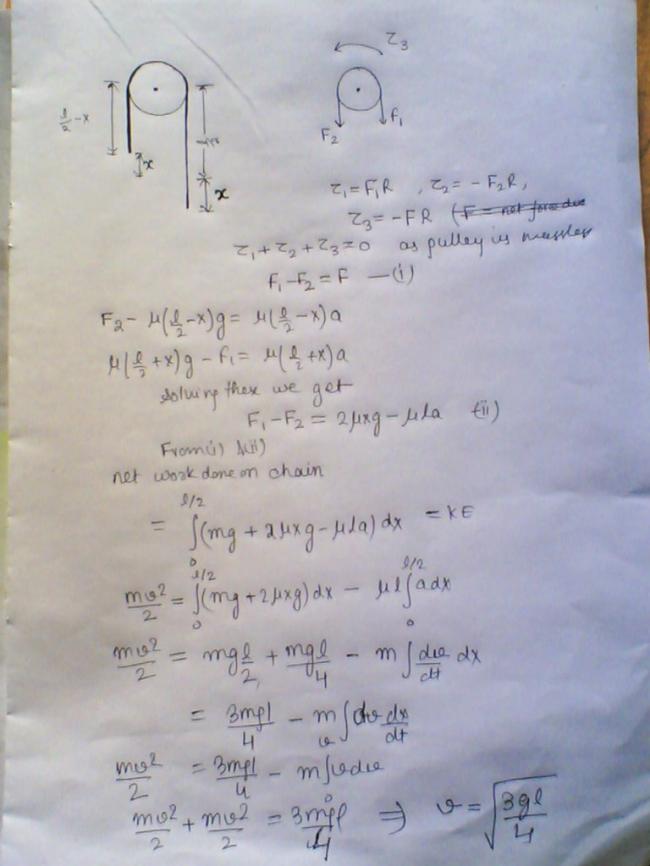
I am not getting anything more than this... nor i am finding any mistake in what i wrote... please someone see...
33@∫dfR over the whole pulley=0
hence ∫df=0 as R≠0
this i think is wrong.... as net torue u are saying for pulley is zero... and have not taken due to weight of hanging chain on both sides..
∫dfR+torque due to weights of chain=0
thats what i wrote in
Force can be zero by hinge... But for torque to be zero..
τ1=μ(l/2-x)gR
τ2=μ(l/2+x)gR
net torque due to these is 2μxgR
so τ3 should be... 2μxgR in anti clock wise..
But i think i made a mistake in writing torque due to wts of chain...
it will be not their wieght as they are accelerted...
Phir se kar ke dekhenge...
11i think this question must be asked by Mr Satan[12][12][12]
daal mein kuch kaala hai
ya poori daal hi kaali hai[3]
1one thing ..
why cant we just cnserve energy an get the answer ?
N is acting perpendicular to all points hence work done by it =0
mg is doing work ..
now if the string sli on the pulle then at each point friction will act behind the directio of motion and hence there will be a torque on the negligible mass
but as m=0 torque should be 0
so it doesnt slip
indicating at each time v=wR
so further let us considre a small mass dm at an ange θ to the horizontal aken clockwise.
on that mss df is acting backwards
if that mass gets displaces by a small length dx to the ightthen work done by friction =-dfdx
but then each dm moves by dx over the pulley
so dW due to friction=-∫dfdx=-dx∫df --- (i)
as we have fixed the displacement
that df is also acting in opposite direction to the pulley.
the smal torque due to df to he pulley=dfR
but et torque shuld be zero so
∫dfR over the whole pulley=0
hence ∫df=0 as R≠0
so in (i) we get dW=-dx*0=0
so no net work by friction too ..
and tension cancels out in pairs
so what the problm in conserving energy???
1yes it should be zero i used that fact i my answer + some equations of motion.
33
But i think this force is there when half chain had slipped..
@satan net torqueon pulley should be zero naa??
waise how u got ur answer?
1by the centre of mass not shifting horizontall you mean to say we should neglect the part of the mass lying over the pulley ?
or just that 2R is very negligible
but you have not mentioned it in the problem .
33But i am not finding any mistake in statement that net torque should be zero for the pulley as m=0.. :(
so an extra torque due to friction should be there... so that extra force...
33
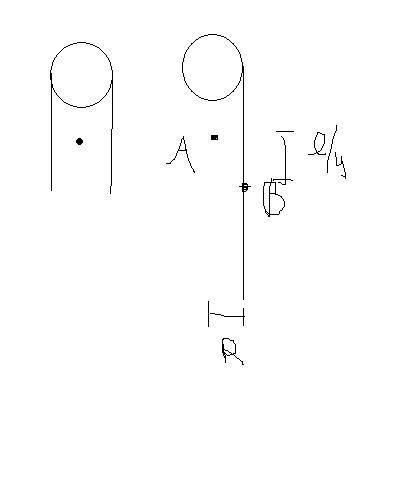
now com not only shifts in downward direction by l/4 but also distance r rightways... so a force must act on rope in right direction...
To search for the force is main point in this question....
I tried this as:...
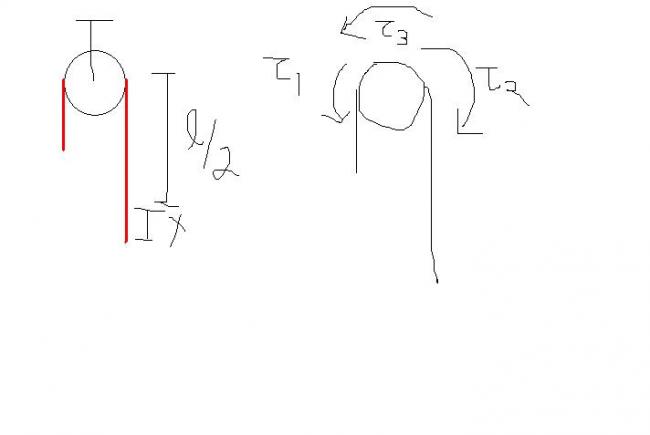
What i did was that since pulley was light m=0
so net torque and force must be zero on it...
Force can be zero by hinge... But for torque to be zero..
τ1=μ(l/2-x)gR
τ2=μ(l/2+x)gR
net torque due to these is 2μxgR
so τ3 should be... 2μxgR in anti clock wise..
for this rope applies a froce (total) 2μxg in radial directions in anticlock wise sense... so on rope a force 2μxg in clockwise sense...
so net force on rope.. =2(m/l)xg+mg
mv2/2=0∫l/2(2(m/l)xg+mg)dx
mv2/2=mgl2/4l+mgl/2
v2=3gl/2
v=√3gl/2.. answer.. please check..
33mv2/2=∫(2mxg/l+mg)dx from 0 to l/2
mv2/2=mgl/4+mgl/2
v=√3gl/2
1priyam......... kidhar gaya aapka post????
delete kardhiya??????????????????????????
62hmm.. okie :)
I thought this was a deeper question :)
where the length wud involve radius and that the horizontal direction's movement wud be involved...
btw I like the profile pic of yours :) who is this? (It seems like a professor who is making fun of students :D)
66No, the radius is not required and we assume the chain (at least, the hanging parts) move only vertically).
62will radius of pulley not be required? and does it have to do with some horizontal component of the velocity?