Please Ignore Post No. 11 And 14 .
f is a real-valued differentiable function defined on [0,1]. If f(0)=0 and f(1)=1, then prove that there exist distinct points x1,x2 in [0,1] satisfying
1/f'(x1) + 1/f'(x2) = 2
-
UP 0 DOWN 0 0 29

29 Answers
I meant to say some x1 , x2 in the interval (0,p) and (p,1) respectively does the job
where f(p) = 0.5
Me dear friend , if " f ( 12 ) ≠12 " , how is equality condition achieved ?
@ Ricky Nice work
I had the following
let f(1/2) = K
so Applying LMVT both sides we get
2K = f'(x1) and 2(1-k) = f'(x2)
so 12K = 1f'(x1)
12(1-k) = 1f'(x2)
so 1f'(x1) + 1f'(x2) ≥ 2 (by AM≥HM)
If f(1/2) ≠1/2 , then also some other x1 , x2 satisfy the equality condition ...
My head obviously agrees with you Sir " :) " , but my heart most certainly doesn't " :( ". Please forgive me for utter nonsense , Sir . . Still , I think my proof's a little bit more " fullproof " , Sir , please respond if you enjoy it as well :) :)
Let another function " g " be defined such that ,
g ( x ) = 1 - f ( x )
It is now clear as water that ,
g ( 0 ) = 1 ............ And g ( 1 ) = 0
So , " g " must have a fixed point lying between ( 0 , 1 ) .
Hence , let that fixed point be " c " .
So , g ( c ) = 1 - f ( c ) = c
Or , f ( c ) = 1 - c .
Apply Langrange's Theorem for two intervals , " ( 0 , c ) " and " ( c , 1 ) " .
Clearly , for some " x1 , x2 " in the respective said intervals ,
f ' ( x1 ) = 1 - cc
And , f ' ( x2 ) = c1 - c
Clearly , " f ' ( x1 ) + f ' ( x2 ) = c1 - c + 1 - cc ≥ 2"
And obviously , " 1f ' ( x1 ) + 1f ' ( x2 ) = 1 - cc + c1 - c ≥ 2 "
Both inequalities are readily established by " AM - GM " inequality , with equality being achieved at " c = 12 " .
I don't know how obvious it is , but spotting the equality condition , I immediately thought of using a point " x " for which " f ( x ) = 12 " in Langrange's theorem and solved the initial question .
Ricky, they would certainly have taught you that when a =2, it is valid to say that a≥2 is also true.
But Sir , how would you prove the first part of the question ? I refer to the first inequality of post no. 15 .
First, Rohan's solution:
By Intermediate Value Theorem, there will exist an xo, 0<x_0<1 such that f(x_0)= \frac{1}{2}
No by Lagrange's, we will find x_1 \in (0,x_0) such that f'(x1) = 1/2xo
and x_2 \in (x_0,1) with f'(x_2) = 1/2(1-x0)
Its easy to see that 1/f'(x1) + 1/f'(x2) = 2.
Now f'(x1) + f'(x2) = 1/2 [ 1/xo + 1/(1-x0) ] ≥ 1/2 X 4 = 2 (by Cauchy Schwarz inequality)
both equalities occur if f(1/2) = 1/2
I am really sorry Sir , but it seems to me as if I don't understand a bit what you are trying to say sir . Can you please write down the full thing , sir ? Obviously I know that you have precious time , but still , if possible , plz do write the solution sir.
You have two inequalities there. In one case its an equality, for the second one, the inequality condition will hold. where's the problem?
But sir , that pair only proves the equality , doesn't it ? Does it prove the inequality as well , sir ?
I said , there is at least one pair of values , not that any " x1 , x2" will satisfy the conditions .
Seems i am not getting ur question..
Actually f'(x) can be negtive , so the least value is not 2 , is it?
Okies , I think I have written some confusing and wrong statements . I 'll restate the problem .
Let " f " be a real valued , differentiable function such that ,
f ( 0 ) = 0 ; And f ( 1 ) = 1 .
Prove that there exists at least one pair of " x1 , x2 E ( 0 , 1 ) " such that , for the above said function , the following inequalities hold simultaneously .
1 . 1f ' ( x1 ) + 1f ' ( x2 ) ≥ 2
2 . f ' ( x1 ) + f ' ( x2 ) ≥ 2
Ever so sorry , both " f ( x 1 ) " and " f ( x 2 ) " have to be positive . Thank you .
Can I make one of my own little extension to this beautiful problem , Bhatt sir ?
My extension - Prove that at least one pair of x1 , x2 exists such that the least value of
" 1f ( x1 ) + 1f ( x2 ) " is 2 .
Also show that , for this pair , the least value of
" f ( x1 ) + f ( x2 ) " is also 2 .
EDIT - Please read post no. 14
if it was given that the function is invertible i had the following
f-1(f(x)) = x lets write f-1 as G
so Gf(x) = x
G'f(x) = 1/f'(x)
Its easy to prove that there exists points x1,x2 such that
G'(f(x1) + G'(f(x2) = 2 = 1/f'(x1) + 1/f'(x2)
but its not given ;(
oh heck, pretty careless of me again. What you said about the fixed pointwould be true if we had for instance, f(0)=1 and f(1)=0. I got mixed up with this. I had the same soln as Rohan's.
I didn't get you sir
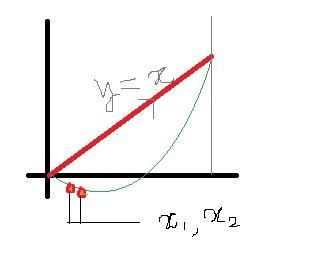
I think i am wrong..there may not exist any fixed point
because G(x) = f(x) - x , G(0) = G(1)= 0 and there exists functions like that ---:D
let c be a point such that f(c) = c 0<c<1
so f(1) - f(c)/1-c = f'(x1)
f(c) - f(0) / c = f'(x2)
we prove both f'(x1) + f'(x2) = 2 and 1/f'(x1) + 1/f'(x2) = 2
@ sir is it right?
Alternative :
there exists a fixed point of F
applying LMVT on both sides and taking reciprocal we get the result..
just take a point between where f(c)=1/2 .. then apply langrange on both sides and sum up the inverted forms of both equations ...