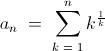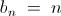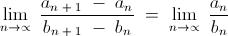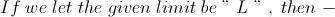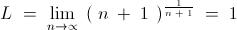\lim_{x\rightarrow \propto } [ 1^{1}+2^{1/2} + 3^{1/3} + ...... + x^{1/x} ]
21Well , there is a test called Ratio Test in Convergence. It says if a_{n}>0 for all n, and \lim_{n\rightarrow\propto}\frac{a_{n+1}}{a_{n}}>1 then \sum_{n=1}^{\propto }{}a_{n} diverges. Hence the limit diverges.
Edit: Ratio test is inconclusive here, since the limit is 1, as shown by kreyszig below.
1\texttt{Let us consider f(x)= }\mathrm{x^{\frac{1}{x}}}\\ \\ \mathrm{f'(x)=\frac{\left( 1-\log{x}\right)}{x^2}f(x)} \\ \\ \texttt{Clearly }\lim_{x \rightarrow \infty } \mathrm{f'(x)=0} \\ \\ \texttt{from this we can infer} \\ \\ \boxed{\lim_{n \rightarrow \infty}\frac{a_{n+1}}{a_n}=1}
21Oh.. Sorry
According to Cauchy criterion If the sequence {a_{n}} is summable it is necessary(not sufficient) that \lim_{m,n\rightarrow \propto }a_{n+1}+...+a_{m} =0. Which implies \lim_{n\rightarrow \propto }a_{n} =0. But here\lim_{n\rightarrow \propto }a_{n} =1 .Hence it diverges.
341Its evident that each of the terms (except the 1st term) >1.
So 1^1+2^{\frac{1}{2}} +...+n^{\frac{1}{n}}>n and hence diverges
262sorry, the question has been mistyped .
\lim_{x\rightarrow \propto } \frac{[ 1^{1}+2^{1/2} + 3^{1/3} + ...... + x^{1/x} ]}{x}
341We have the bounds
1=\frac{n}{n} < \frac{1^1 + 2^{\frac{1}{2}}+...+n^{\frac{1}{n}}}{n}< \frac{n \times n^{\frac{1}{n}}}{n} = n^{\frac{1}{n}}
Also \lim_{n \rightarrow \infty} n^{\frac{1}{n}}=1
By Sandwich principle, the limit is 1
1Sir , don't you think that -
3 1 / 3 > n 1 / n ,
for any " n " ?
All I am saying is Sir , is that the limit is crunched between " 1 " and " 3 1 / 3 " , not " 1 " and " 1 " .
341After your post, I realized that this is simply an application of
http://targetiit.com/iit-jee-forum/posts/a-beautiful-problems-18777.html
1http://targetiit.com/iit-jee-forum/posts/a-beautiful-problems-18777.html
The solution is trivial even without using the Cesaro - Stolz theorem . Just Transform the sequence " cn = 1n " into the new sequence " an cn " ( where " an " is defined in that thread ) using Toeplitz Transformation , and that does the trick .
