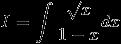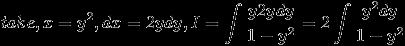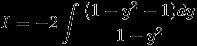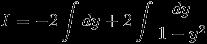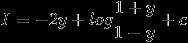mkm

evaluate

" WITHOUT USING TRIGONOMETRIC SUBSTITUTION "

1) I = \int_{0}^{\pi /2}{\frac{sinx}{1+cosx+sinx}}dx ....................(1)
also I = \int_{0}^{\pi /2}{\frac{cosx}{1+cosx+sinx}}dx .......................(2)
by using property \int_{a}^{b}{f(x)}dx=\int_{a}^{b}{f(a+b-x)}dx

now adding both (1) and (2) we get :
2I = \int_{0}^{\pi /2}{\frac{sinx+cosx}{1+sinx+cosx}}dx = \int_{0}^{\pi /2}{\frac{1+sinx+cosx-1}{1+sinx +cosx}}dx

2I = \int_{0}^{\pi /2}{\frac{1+sinx+cosx}{1+sinx+cosx}}dx -\int_{0}^{\pi/2}{\frac{1}{1+sinx+cosx}}dx
now let I_{1}=\int_{0}^{\pi/2}{\frac{1}{1+sinx+cosx}}dx

now expand sinx as 2tanx1+tan²x and cosx as 1-tan²x1+tan²x and sustitute tanx2 = t we will get the ans.

fantastic solution by manmay

2) substituting √x = t we get dx = 2t dt
now it's easy i guess.