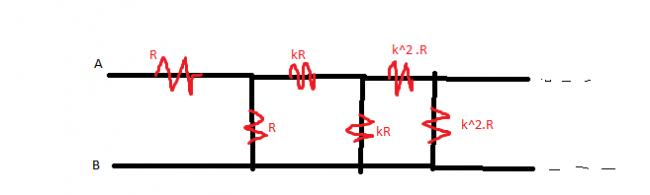
calculate the equivalent resistance across A B of this infinitely long ladder
30This is my hunch, and I'm following my hunch purely.
C_{eq}= R+\left(\frac{1}{R}+\frac{1}{kC_{eq}}\right)^{-1}
We get the following equation,
kC_{eq}^{2}-RC_{eq}\left(2k-1\right) - R^{2} =0
C_{eq}=\frac{R(2k-1) \pm R\sqrt{4k^2+1}}{2k}
This is what I could get to. [7]
262yes , your ans is right!
i didnt get ur first step .
C_{eq}= R+\left(\frac{1}{R}+\frac{1}{kC_{eq}}\right)^{-1} ??
21since its an infinite ladder ...see examples of hcv (capacitor or resistance)
30Well.. what nasiko says is right. Thats how I approached the problem. The logic comes from the old problem in maths,
y=\sqrt{2+\sqrt{2+\sqrt{2+...}}}
where we rewrite the equation as,
y=\sqrt{2+y}
The good thing abt the question you posted is that at first look, it seems difficult to spot this trend. But then, if we take k common from the third resistance onwards, we seem to be getting the trend we reqd.
More mathematically,
C_{eq}=R+\left(\frac{1}{R}+\frac{1}{kR+\left(\frac{1}{kR}+\frac{1}{k^2R+..}\right)^{-1}}\right)^{-1}
C_{eq}=R+\left(\frac{1}{R}+\frac{1}{k\left(R+\left(\frac{1}{R}+\frac{1}{kR+..}\right)^{-1}}\right)\right)^{-1} \Rightarrow C_{eq}=R+\left(\frac{1}{R}+\frac{1}{kC_{eq}}\right)^{-1}
262thnx Ashish ,
even i had tried that recurrence but made a mistake !