At time t=0 string A is cut, then what will be the maximum compression in the spring if spring constant is K.(Assume surfaces are smooth and initially spring was at its natural length)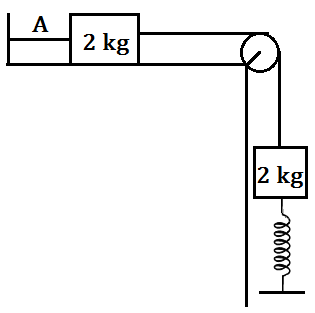
-
UP 0 DOWN 0 1 4
4 Answers
5352gk
Akash Anand Wrong answer I guessUpvote·0· Reply ·2014-03-21 23:08:25
486At the mean position, Kx=2g; x=2gK
2gx=12Kx2 +K.E (Using energy conservation)
K.E is the kinetic energy of the two block system ,individually they each have kinetic energy=K.E2
Just after that the string would become loose,So the upper block would continue to move with that velocity,
So at max. compression(h) the kinetic energy of system=K.E2
2gh=12Kh2 +K.E2
Solving we get,h=(2+√2)gK
IS IT CORRECT?
Himanshu Giria At mean position x wu 0 i guess d b = to- Himanshu Giria at mean position i guess x wud b =0...
- Niraj kumar Jha After cutting A ,"mean position" means when the net force on lower block is zero.
- Akash Anand After the mean position, by COE loss in P.E + Loss in K.E would be equal to the P.E stored in the spring na??
- Niraj kumar Jha Sir, we can also do that and the obtained ans. should be addded to 2g/K to get max. compression.but I took initial point as point of reference and as initially there was no K.E
Loss in P.E=K.E at max. comp.+P.E stored in spring.the result here directly gives max. comp.
1161Niraj..I am not able to find the fallacy, but the given answer is far different from this. Given answer is 0.45m .
- Niraj kumar Jha Sir, answer isn't in even in terms of "K"?
- Akash Anand Actually K is given 100N/m.