Three sound waves of equal amplitudes have frequencies

Please be patient and read the solution

Ans-2

I assume that you know the basics of beat.

Beats is interference of two or more waves with a little difference in frequency. The rest is same i.e., the medium, the initial phase and the direction of propagation

Consider a beat formed by two waves-

y₁ = A sin (wt - kx) and y₂ = A sin (Wt - kx) [with frequencies w and W]

Equation of beats is the trajectory of the particle at origin.

so, y(net, x=0) = A sinwt + AsinWt= 2A cos[(w-W)t/2] sin[(w+w)t/2]

At t=0, y₁ = y₂ = 0 (due to phase)

So, at t=0, y_net,x=0 = 0, due to phase.

As y(net, x=0) = 2A cos[(w-W)t/2] sin[(w+w)t/2]

and at t=0, sin[(w+w)t/2] is zero, the sine function is phase.

So, particle at origin oscillates with Amplitude = 2A cos[(w-W)t/2 Phase function = sin[(w+w)t/2]

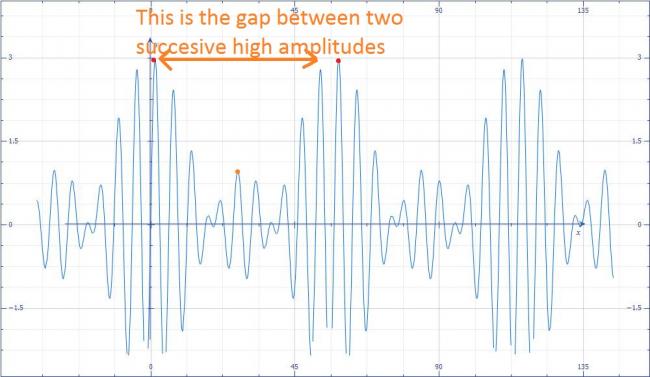
If you observe the plot of beats, the Amplitude (Cosine function) in its period, takes Maximum values when Cos gives +1 or -1. So, in one cycle of Cosine function, there are two Amplitude extremums- Maximum magnitude i.e., Amplitude is maximum twice in one cycle

In a beat, there is only one Amplitude maxima, i.e., Amplitude is maximum only once in once cycle.

If the time period of Amplitude is T(A), time period of beats is T(b)=T(A)/2 as in one cycle of Amplitude function, there are two cycles of beats.

If frequency of Amplitude function is V(A), frequency of beats is V(b) = 2V(A)

Now the question-

waves are

y₁ = Asin (wt - kx); w=2Î v

y₂ = Asin (w₂t - kx); w₂=2Î (v-1) = 2Î v - 2Î = w - 2Î

y₃ = Asin (w₃t - kx); w₃ =2Î (v+1) = 2Î v + 2Î = w + 2Î

As per the derivation;

y(net, x=0) = A [sin wt + sin w₂t + sin w₃t ]

= A [ sin wt + sin (w - 2Î )t + sin (w + 2Î )t ]

=A [sinwt +2 sin(wt) cos(2Î t)]

=A[1 + cos2Î t] sin wt

Amplitude Function = A[1 + cos2Î t] = f(t)

As the function is simple a cosine function, the period can be found very easily. Let it be T,

f(t)= f(t+T)

or A[1 + cos2Î t] = A[1 + cos {2Î t + 2Î T}

or 2Î T=2Î

or T=1s

the amplitude has a time period of 1 second. As the amplitude is simple cosine formula, the time period of beats T(b) is T/2=1/2s as discussed above

Frequency of beats= 1/T(b)

=2 per second

Answer is 2

Same type question is repeated for NEET 2016 phase2.

There the answer is 2

AKHIL is right....The answer is 2

Max number of beats=(v+1)-(v-1)=2

I saw the answer is Fiitjee's problem package that it is 1 ? Don't know how?

Ab ye kya hai?

Need more comments!

1st of all this is AIEEE 2009 quesn , not of 2010!!

secondly , i hav seen 2 3 coaching institute's solns.
in all the ans given is 2..

The answer of this question is 1

It's given in HCV as well. Here it is -

" Beyond a certain proximity (usu. about 15 Hz), beating becomes undetectable and a roughness is heard instead, after which the two pitches are perceived as separate. "

Well when three or more frequencies are given, and we require to find the beat frequency, we find the maximum difference in frequency. So in this case beat frequency is 2. If the maximum difference is large enough and doesn't produce beats , then we look for the next maximum difference.