I am getting \hspace{-16}\mathbf{3^{\frac{1}{3}}}$
Determine the largest number in the infinite sequence
1^1/1 , 2^1/2 , 3^1/3 , 4^1/4 , ............ n^1/n
-
UP 0 DOWN 0 0 8

8 Answers
Yes it is.
Proof: Let a function f(x)=x^{\frac{1}{x}}
The maxima will occur at the point where f'(x)=0 and f"(x)<0
We get,
\frac{d}{dx}(f(x))=x^{\frac{1}{x}-2}(1-\ln x)
So, f'(x)=0 for x=e≈2.71...
And we can prove f"(x)<0
Since 3 is the closest integer to e 3^(1/3) sholud be least.
and you can also check the graph.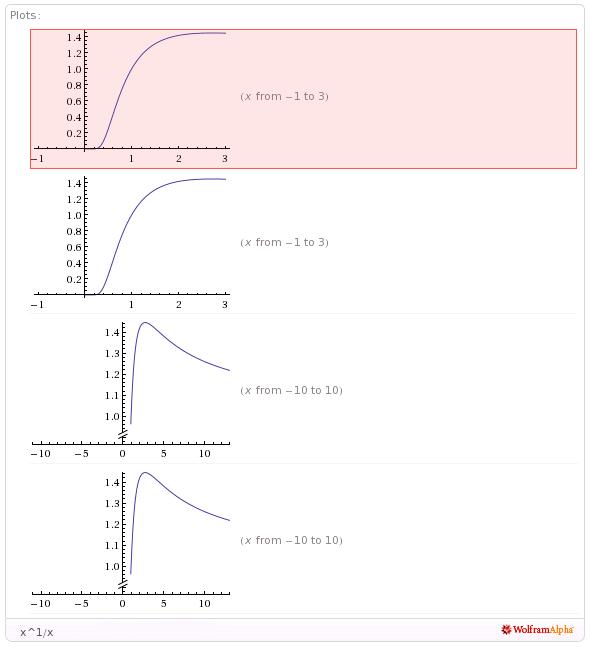
plz solve this question without using concepts of differentiation....
i dont know calculas...
n(n+1) ≈ (n+1)n
n ≈ (1+1/n)n
n ≈ 1 + 1 + terms less than 1 each...
if u see the last 2 terms they will together be less than 1 when n is greater than 3
so it is clearn that LHS is greater than RHS
so we can say
n(n+1) > (n+1)n
if n >3
by simple check we can get that among n = 1, 2, 3 n=3 is the largest
ameyaloya have u cleared RMO 2?
are you from pune?
in which yr did it appear in INMO?
@ shubhodip
yes i cleared rmo2.
i m not from pune ; i live in aurangabad in maharashtra.
this question nappeared in inmo 1990.