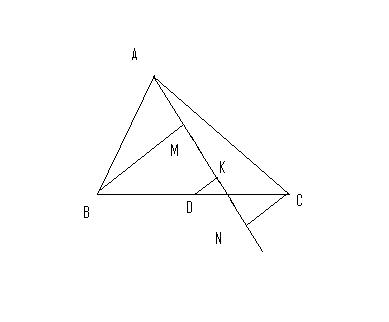
let BC & AN meet at O.
now, ΔMOB≈ΔKOD≈ΔOCN
MK/BD=KO/OD=ON/OC=KN/CD. as CD=BD so MK=KN so MD=DN.
[proved]
Let AN be any line drawn through A in a Triangle ABC.
Let BM, CN perpendiculars are drawn from B and C to AN and let D be the mid-point of BC, prove that MD = ND.
-
UP 0 DOWN 0 1 17

17 Answers
can't get ur soln....
either the problem lies with the literature of my question or maybe u r wrong...
here's the exact question with the figure once again......

Given a triangle ABC. A line from A meeting BC at O is drawn.
perpendiculars are drawn on AO from B and C at M and N respectively.
If D is the mid point of BC then prove that,
DM = DN
Denote the intersection of MN and BC by O
since BM || NC
ON/ OC = OM/OB = (ON + OM)/(OC + OB) = MN/BC = MF/BD
so OM/OB = MF/BD = (OM- MF)/(OB - BD) = OF/OD
so OF/OD = MF/BD so the result follows by thales
(No construction, nothing )
well my soln. using Apollonious..!!

The red lines are the contructions i've done..!!
Now, using Appolonius theorem...
In triangle ABC we have,
BM2 + CM2 = 2 (BD2 + DM2) --- (i)
And, in triangle BNC we have,
BN2 + CN2 = 2 (BD2 + DN2) ---- (ii)
on (i) - (ii) we have,
BM2 - BN2 + CM2 - CN2 = 2 (DM2 - DN2)
=> - MN2 + MN2 = 2 (DM2 - DN2)
=> DM = DN
what's wrong with u??????
In triangle BOM , "D" is not the mid point of OB...!!
How then can u say DF || BM ???????
actually i've already done this question with Apollonius
And here goes the Thales' theorem...

and what u r trying to say is...

Here, F is the mid point of MN , D is the mid point of BC
then which part of Thales' theorem says DF || BM
rather, if D would have been the mid point of A line through N which would meet
BM at some point then one could say, DF || BM...
nd i don't knw what r u trying to do?????
if u can prove it using thales' theorem by constructing triangles and all then do it....
i just want to see the proof....
that's all....!!
(Breaking the promise)
F is the mid point of MN
then BM || DF || NC
What the hell is wrong here ?
Can't you just try to prove BM || DF || NC ?
i think the concept that u r using here is cent % wrong....
nd has no relation with thales' theorem.....
jst look at the statement uv posted..
nd thats wht iv been trying to tell u...
(for the last time )
Let F be the mid point of MN
DF ||BM || NC (if u cant get this by thales, use complex number/coordinate )
so MN perpendicular to DF, F is midpoint so FD is it's perpendicular bisector ; so DM = DN
This is extremely easy, it probably reduces to the fact that , in isosceles triangle ABC, C lies on the perpendicular bisector of AB
F is midpoint of MN, D is mid point of BC
BM || NC
so BM ||NC || DF (use thales)
@shubhodip couldnt get...can u please explain?
@rahul can u give the solution.. y r images not being uploaded properly?? this is annoying ...
what?
how can DF||BM||CN by ur statement?
afterall u can't make the median perpendicular to MN from D unless u prove the statement
either
DM = DN (That's what u need to prove)
or,
that DF bisects angle MDN..
cun't get... explain please..!!
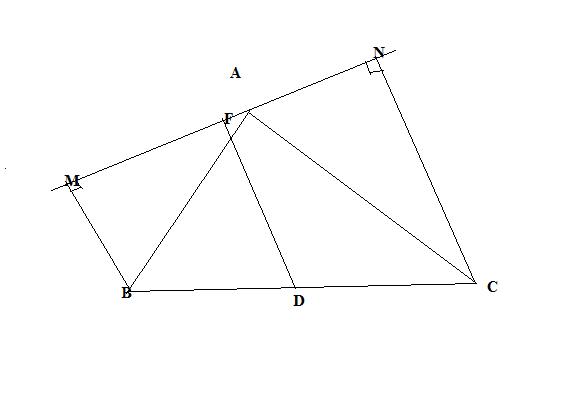
idk if u can see the image, at least I don't
Let F be the midpoint of MN
so DF || BM || CN
so MN perpendicular to DF, F is midpoint so FD is it's perpendicular bisector ; so DM = DN
@Shubhodip - i don't think so... can u show ur work?
@Anik - try to figure out what the statement says... its easy..!!