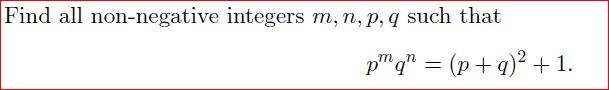I think there are none.
11 Answers
I can give an idea(although i haven't solved the problem completely). first we consider that one of the $p,q$ is equal to 1 an then solve it (i think it will not be too hard).now we observe that $p$ and $q$ are relatively prime..We suppose that both m and n are greater than 2 and then a trivial inequality will lead to the conclusion that both of them should be at most 2.now we check each cases and i think we will arrive at some satisfactory conclusion.
Nope..there r solutions..
I read this one mathlinks , probably IRAN TST q and was also in INDIAN Postal coaching.. :P
there will be infinite number of solutions for this. because it is not given that they r unique.so put m,n=0 then we get p=1/q which has many solutoins for p and q. i am not sure bt hope to be correct
May be there are in that case Shubho, I guess I'll have to recheck, perhaps...
BTW can you give me the link? I mean I kind-off still feel there cannot exist solutions to this....
I AM A NEW USER HERE........
SO I CANNOT MAKE FOORUM.
PLEASE ANSWER ME WHICH ONE IS BETTER IN CASE OF SALARY AND JOB SECURITY CIVIL OR CHEMICAL. GOD
Ah - so silly of me!
The eqn is just p2q2=(p+q)2+1
Along with the odd restriction pq=5
:P