Find all continuous functions f satisfying $$ 3f(2x+1)=f(x)+5x.$$
Prove that for $$a,b,c>0$$
$$\frac{1}{2a^{2}+bc}+\frac{1}{2b^{2}+ca}+\frac{1}{2c^{2}+ab}\leq \left( \frac{a+b+c}{ab+bc+ca}\right) ^{2}.$$
-
UP 0 DOWN 0 0 9

9 Answers
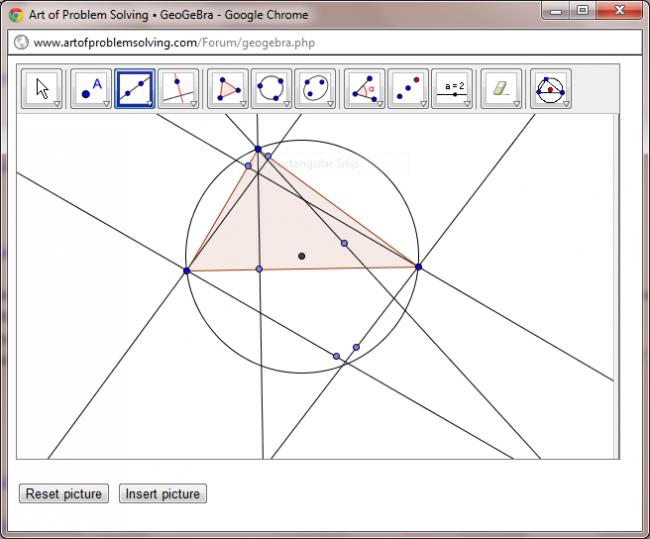
In a triangle $$ABC$$, If $$L,M,N$$ are the foot of perpendicular from respectively to the opposite sides. If $$s,S''$$ be the semi perimeters of $$LMN , ABC$$ respectively, the show that s\leq \frac{S}{2}.
Of Course, But you would want to write some more in a RMO!
@ Vivek Thank you for the problems.
2.http://www.artofproblemsolving.com/Forum/viewtopic.php?f=46&t=449593 See this here is a wonderful solution of Learner 94.
Which kills the problem.
@Arnab, For which question you have posted the solution link and figure. I seem the one I posted in 3 and the one you have linked aren't same.
1. Solution
Using the Cauchy Schwarz Inequality we have :
(2a^+bc)\left[\frac{(b+c)^{2}}{2}+bc \right] \geq (ab+bc+ca)^2
\frac{1}{2a^2+bc}\leq \frac{\frac{(b+c)^2}{2}+bc}{(ab+bc+ca)^2} =\frac{\frac{(b^2+c^2)}{2}+2bc}{(ab+bc+ca)^2}
Adding this and its analogous inequalities, the conclusion follows. Equality holds
iff a=b =c.