A solid iron sphere of radius=1m is just submerged in a water tank. A point source of light is kept vertically above its center at a distance 1m from the water surface.
Find the area of the sphere's shadow. Refractive index of water=1.414.
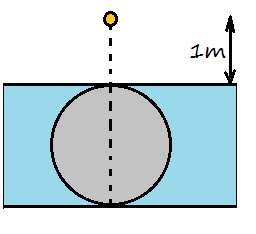
1133sinisinr = 1.414
i = 90-r2
Use wolframalpha to solve the first equation.
http://www.wolframalpha.com/input/?i=sin%28%2890-x%29%2F2%29+-+1.414*sin%28x%29+%3D+0
Area: π[2tanr + cot(90+r2)]2
Anurag Ghosh Thanxx..:)
Akash Anand I guess Shashwat has done it in a different way..Shashwat ... do you still have that solution?
2305I don't have that solution anymore.
Neither do I have that question anymore.
But anyways the solution below is somewhat similar.
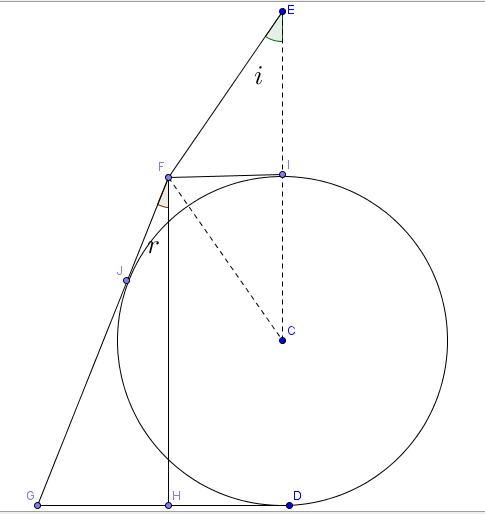
sin(i)sin(r)=μ....(1)
The triangles FEI and FCI are congruent.
→ <FCI =<FEI = i
→<HFC = <FCI = i(Alternate angles)
Since FI and FG are tangents drawn from the same point (F) to the circle.
<IFC = <CFG = i+r
<IFH = <IFC +<CFH = i+r + i=2i+r=90°....(2)
Tangents drawn from a point to a circle are of equal lengths.
Using this property,
FI = FJ and GD = GJ
Therefore,
FG = FJ+GJ = FI+GD = FI + GH +HD =2FI+GH (Because HD = FI)
→2sec(r) = 2tan(r) + 2tan(i)
→ 1=sin(r)+sin(i)cos(r)cos(i)
→1=sin(i)μ+sin(i)cos(90-2i)cos(i)
→1 = sin(i)μ+2sin2(i)
This is a quadratic in sin(i).
Out of the 2 roots we need to take the positive root.
Than we can find sin(r) from equation(1).
The length GD = GH+HD=2tan(r)+tan(i)
And area = π(GD)2
Akash Anand Excellent..