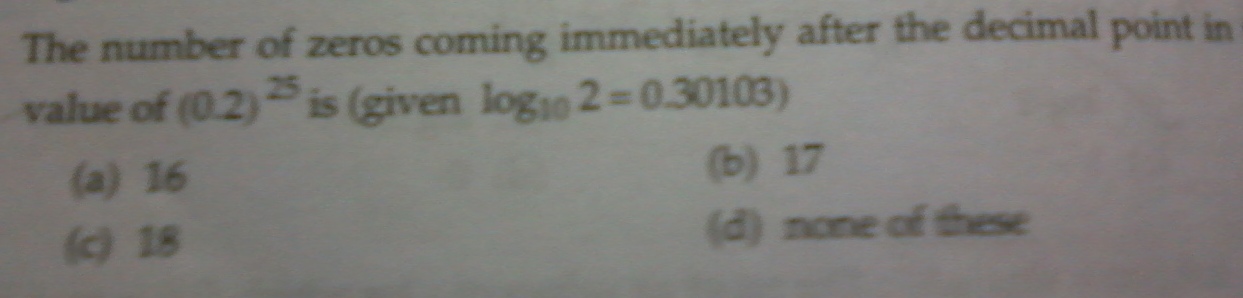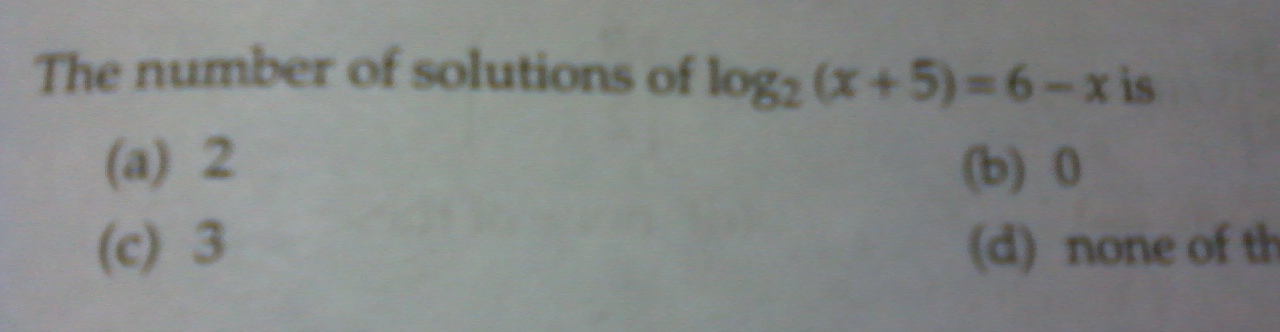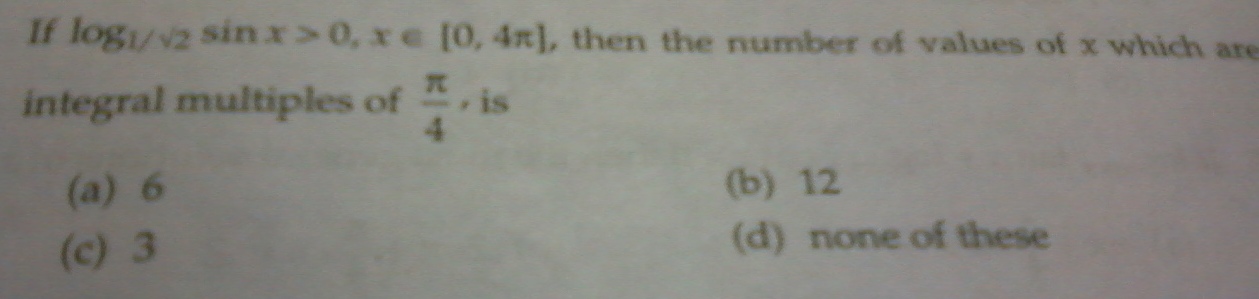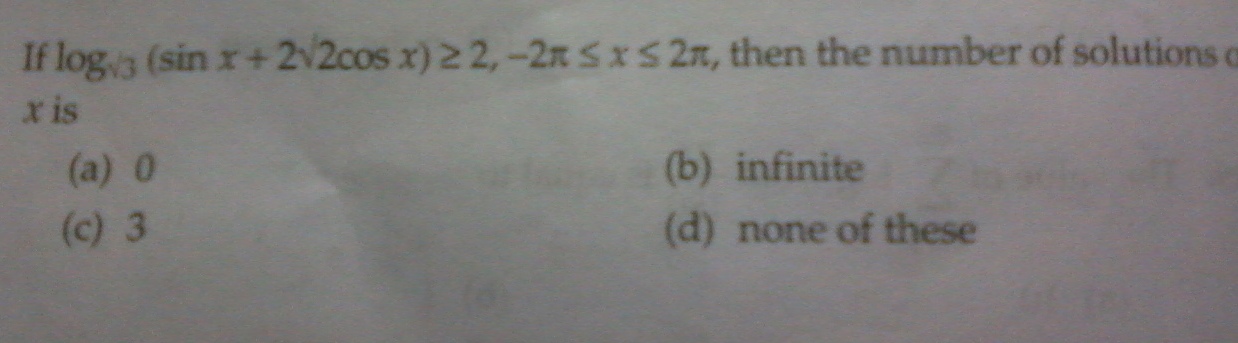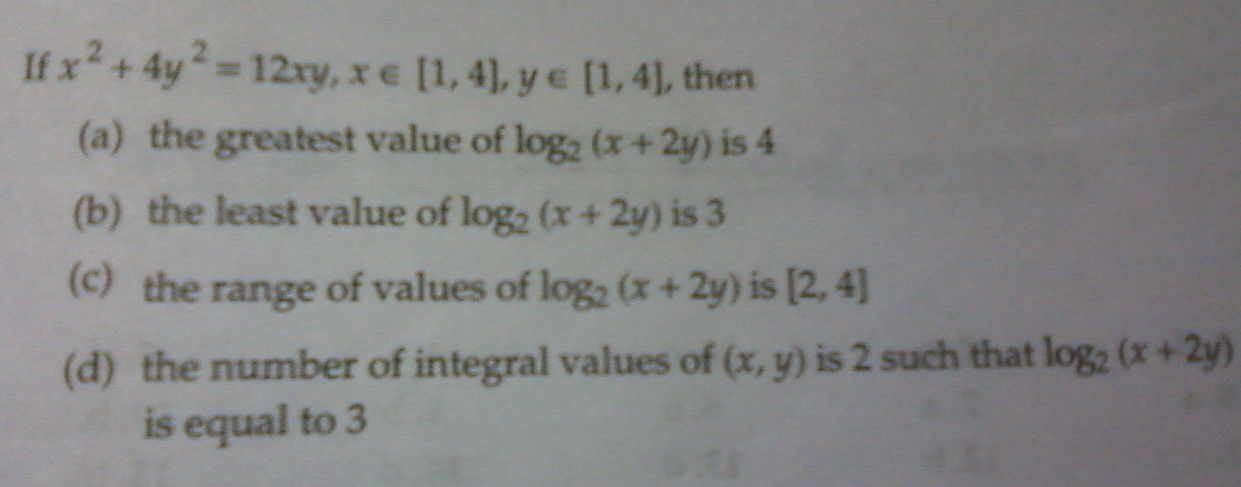LOGARITHM

2. Draw a rough graph of y = log₂(x+5) and y=6-x.
You'll see that they intersect once. Thus the given eq. has one solution.

3. log_1/√2(sinx) > 0
→log_2^(-0.5) (sinx)>0
→(-1/2)log₂sinx>0
→log₂sinx<0
→sinx<1

Simultaneously sinx>0 (domain)

only one value of x satisfies the given relation in [0,pi/2] which is pi/4

Thus in [0,4pi] there will be 4 solutions.
2 in [0,Ï€]
0 :[Ï€,2Ï€] ; 2 :[2Ï€,3Ï€] ; 0:[3Ï€,4Ï€]

4. Proceeding similarly as in the previous sum, you will see that the ineq. reduces to sin(x+θ)≥1 where cosθ=1/3

Therefore, x+θ=π/2
or, x = asin(1/3)

In [-2Ï€,2Ï€] there will again be 4 values of x.
Answer should be D.

Q. 1:- (0.2)²⁵=2²⁵x10^-25. Now, log₁₀2²⁵≈7.5 which means that there are 8 digits in 2²⁵. In 10^-25, after the decimal point, there are 24 zeroes and one 1, that is 25 digits. So, in (.2)²⁵, the last 8 digits will be of 2²⁵ and the 17 before that will all be zero. (B).

Q. 5:- x²+y²=12xy or, (x+2y)²=16xy. Now, log₂(x+2y)²=log₂(16xy)=4+log₂(xy). For the given range of x and y, log₂(x+2y)² lies between 4 and 8. So, log₂(x+2y) lies between 2 and 4. →(C).
It is apparent that for the logarithm to be 3, xy=4 and the ordered pairs are (4, 1), (2, 2), (1, 4). So (D) is not correct.