Calculus - some questions...

1708

(1)

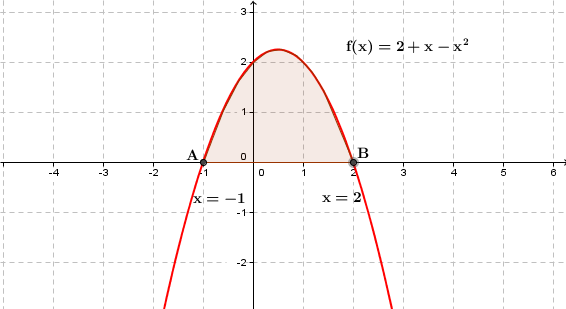
$\hspace{-16}$So from graph Area is Maximum when $\bf{a=-1}$ and $\bf{b=2}$$

(2)

$\hspace{-16}$Here $\bf{f(x)=\frac{6}{1+31e^x}\; \forall x\in \mathbb{R}}$\\\\\\ Now $\bf{\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}\frac{6}{1+31e^x}\rightarrow 6}$\\\\\\ and $\bf{\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}\frac{6}{1+31e^x}\rightarrow 0}$\\\\\\ and $\bf{f(x)}$ is a Cont. function. So $\bf{f(x)\in \left\{1,2,3,4,5\right\}}$\\\\\\ So Total $\bf{5}$ distinct values of $\bf{f(x)}$ exists.$

(3)

$\hspace{-16}$Given $\bf{\lim_{x\rightarrow \infty}\sqrt[3]{\bf{8x^3+mx^2}}-nx = 1}$\\\\\\ Now put $\bf{x=\frac{1}{y}}$ and $\bf{y\rightarrow \infty}$\\\\\\ $\bf{\lim_{y\rightarrow 0}\frac{(8+my)^{\frac{1}{3}}-n}{y}=1}$\\\\\\ Now for the existance of limit, Limit must be $\bf{\frac{0}{0}-}$ form.\\\\\\ So $\bf{\lim_{y\rightarrow 0}(8+my)^{\frac{1}{3}}-n = 0\Leftrightarrow n=2}$\\\\\\ So $\bf{\lim_{y\rightarrow 0}\frac{(8+my)^{\frac{1}{3}}-2}{y}=1}$\\\\\\ $\bf{\lim_{y\rightarrow 0}\frac{2.\left(1+\frac{my}{8}\right)^{\frac{1}{3}}-2}{y}=1}$\\\\\\ $\bf{\lim_{y\rightarrow 0}\frac{\left(1+\frac{my}{8}\right)^{\frac{1}{3}}-2}{y}=\frac{1}{2}}$\\\\\\ Using expansion of $\bf{(1+x)^n}$\\\\\\ So We Get $\bf{m=12}$\\\\\\ So $\bf{m+n = 12+2=14}$$