1. if a1 , a2 , a3 ... a7 are seven not necessarily distinct real numbers such that 1<ai<13 , prove that we can construct a triangle with its sides with length ai
2 If Nn denote the nth son square integer so that N1=2 , N2=3 , N3=5 and so on and m2<Nn<(m+1)2 then show that m=[√n + 1/2]
this was proved by prophet sir few days back here http://www.targetiit.com/iit-jee-forum/posts/nice-one-from-isi-2009-18650.html
3. Prove for all nεN 3)(3/4(1/2)(2/)...((2n-1)/2n) < 1/√(2n+1) (not sure if remember correctly)
4. If R and S represent cubes of sides r and s where r,s are integers such that difference between the volumes of the cubes equals that between their surface area, show that r=s
5. What can you say about a so that sin(√(x+a))=sin√x for all real x>0. Justify
there were three more problems(my friend doesnt remember those) and one had to do six in 2 hours
These questions may not be complete as they are as recalled by my seniors
looks like ISI straightaway picked up the 2nd one from prophet sirs post here note even the letter 'm' was unchanged http://www.targetiit.com/iit-jee-forum/posts/nice-one-from-isi-2009-18650.html or it seems like prohet sir was one of the paper setters(high probability) :):)
1Heres my solution for the first one
if 3 or more of the ai's are equal, we can easily form an equilateral triangle. so assume not more than 2 ai's to be equal.
divide the interval (1,13) as follows
(1,5] , (5,9) , [9,13)
using pigeon hole principle, atleast three of the ai's lie in the same interval which can be used to form a triangle.
third one seems an exercise on induction. please post your solutions people
1ALL THE MIB questions are avaiable on http://www.artofproblemsolving.com/Forum/viewtopic.php?f=513&t=405632
21solution to 1.
Geometry will make it easier to explain.
a)slope of a line can be any real number. we represent all ai's by a line passing through the origin with slope ai
b)The angle between the line with slope 1 and 13 is divided in six equal angels of value tan-1(1/7)(there are boxes)
3)By PHP at least 3 lines must lie in same box. they will look like
We can form a triangle with their slopes.
4)It's trivial to see that slope of A + slope of C > slope of B
and slope of A + slope of B > slope of C
It remains to prove that slope of B + slope of C > slope of A
It will be sufficient to prove that
2tan(tan-1(n/7) ≥ tantan-1((n+1)/7) ,where n= {1,2,3,4,5}
which is very obvious.
So we have proved.
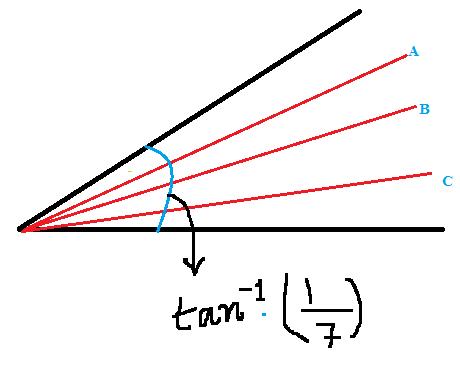
1@ shubhodip pls explain step 3.
i noticed a serious mistake in my proof for 1. three ai's in (1,5] does not gurantee a triangle
heres a solution to another question i forgot to mention earlier
6. if t1<t2<t3<...<t99 be ninety nine real numbers, show that f(x) = lx-t1l + lx-t2l + ... + lx-t99l attains minima at x=t50
SOLN: Divide the domain of x into the following
(-∞,t1] , (t1,t2] , (t2,t3] , ... , (t99,∞)
for xε (-∞,t1) , f(x) = K1 - 99x (K1 is a constant)
for xε [t1,t2] , f(x) = K2 - 97x
.
.
.
for x=t50 , f(x) is a costant I
for xε (t50,t51 , f(x) = x + K51
.
.
.
for xε (t99,∞) , f(x) = 99x + K100
so on a graph , f(x) looks like
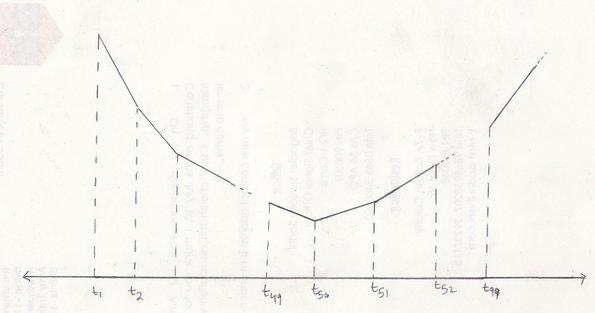
so slope ie f'(x) changes its sign from negative to positive at x=t50 hence it is a point of minima.
21I have also made mistake.
Actually i think the 7 real numbers chosen are between 2 and 12.
(according to soulhunter on Mathlinks)