11
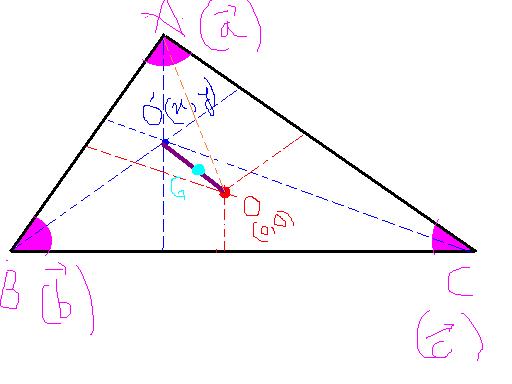
Let the vertices of the triangle ABC be A (a) ; B (b) and C (c) w.r.t origin.
Let O ' (x,y) be the orthocentre and O (0,0) be the circumcentre (origin).
Let G be the centroid.
Thus G\ =\ \left(\frac{\vec{a}\ +\ \vec{b}\ +\ \vec{c} }{3} \right)
Since the centroide G divides the orthocentre C (x,y) and circumcentre (0,0) in the ratio 2 : 1 , thus by using section formula , we get
\left(\frac{\vec{a}\ +\ \vec{b}\ +\ \vec{c} }{3} \right)\ =\ \frac{2\ (0)\ +\ OO'}{3}
Thus, we get
\vec{a}\ +\ \vec{b}\ +\ \vec{c}\ =\ OO'
or
OA + OB + OC = OO'
Thus, (i) proved.
(ii) Now, consider triangle AOO' ,
using the rule of vectors addition , we get
O'A\ = O'O\ +\ OA
O'A\ = O'O\ +\ \vec{a} .......................(ii)
Similarily, we get
O'B\ = O'O\ +\ \vec{b} .....................(ii)
&
O'C\ = O'O\ +\ \vec{c} .....................(iii)
From (i), (ii) and (iii), we get
O'A\ +\ O'B\ + \ O'C\ = 3\ O'O \ +\ (\vec{a}\ +\ \vec{b}\ +\ \vec{c})
Since Since\ \vec{a}\ +\ \vec{b}\ +\ \vec{c}\ =\ OO'
Thus, we get
O'A + O'B + O'C = 2 OO'
Thus proved
