4.is it possible????????
SHARE:
1. Let N = 1111 ........ 11 {1998 times}, then find the 1001th digit after decimal for √N.
DOUBT:
2. \textup{If } \frac{1}{1! 11!}+\frac{1}{3! 9!}+\frac{1}{5! 7!} = \frac{2^{n}}{m!} \textup{and } f\left(x+y \right) = f\left(x \right).f\left(y \right) \textup{for all x,y}
\texttt{and } f\left(1 \right)=1,f^{'}\left(0 \right)=10,\textup{then}:
A) f'(n) = m
B) f'(m) = n
C) f'(n) ≠f'(m)
D) NONE
3. P is an orthogonal matrix and A is a periodic matrix with period 4 and Q = PAPT then X = PTQ2005P will be -
A) A
B) A2
C) A3
D) A4
4. Find no/nos satisfying abcd * 4 = dcba ?
-
UP 0 DOWN 0 0 14

14 Answers
That is what we have to search!!
One more Doubt:
Please provide a simpler simplification of this 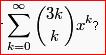
4. Dunno what the procedure should be, but 2178 is the only 4-digit number satisfying that...
I made a program in C++ to find out :P
@Pritish Bhaiya,
Can you please HIDE post that C++ program. I need that!! Or even in my chatbox
And yes it's correct! But I'll wait for sir to post the procedure besides hit and trial method!
4)
Start with some inequalities:
1 <= A <= 9 (since ABCD is a four-digit number, A can't be zero)
0 <= B <= 9
0 <= C <= 9
4 <= D <= 9 (D must be at least 4*A which is at least 4)
Then we have some equations:
4*D = 10*z + A (z is the carry to the tens column)
4*C + z = 10*y + B (y is the carry to the hundreds column)
4*B + y = 10*x + C (x is the carry to the thousands column)
4*A + x = D
There are more inequalities:
0 <= z <= 3
0 <= y <= 3
0 <= x <= 3 (because the multiplier is 4, the largest a carry can be
is 3)
Now we combine the first and last equations by multiplying the last by
4 and substituting for 4*D in the first equation:
4*(4*A + x) = 10*z + A or 4*x = 10*z - 15*A = 5*(2*z - 3*A)
Since 5 divides the number on the right, 5 must divide 4*x, and
so 5 divides x. But x is small, from 0 to 3, so x = 0 is forced. Thus
2*z - 3*A = 0, so 2*z = 3*A.
Similarly, 3 divides z, so put z = 3*w, so A = 2*w.
Then D = 8*w, and 4 <= D <= 9.
Clearly D = 8, so w = 1, A = 2, and z = 3.
Similarly, using the middle two equations, we can determine B, C, and
y. This gives you the answer you seek. You can finish the rest.
source: http://mathforum.org/library/drmath/view/56759.html
2nd >
multiplying 12! in the numerator of LHS given u terms in the form of 12Ck
i.e LHS is 12C1+12C3+12C512! = 102412!
so n = 10 , m = 12
now f(x+y) = f(x)f(y)
put y = 1 , so f(x+1) =f(x)
hence f(x+n)=f(x)
so f'(x+n)=f'(x)
hence f ' (integer ) = f'(0) = 10 = n
hence b is correct
I'm posting my solution for the first one. There are two : One uses Binomial and other was just a luck by chance solution. I hope the guys out here will figure out the Binomial one as it involves mere calculation, but the LUCK BY CHANCE one is really great.
Soln:
We observe √11 = 3.3166....
√1111 = 33.3316666....
and so on.
Hence, N number of 1's in √N gives N2 3's after decimal then 1 and then N 6's {See Above}
Hence when N = 1998, We have
√N = (N-1) .{ N2 3's }{ 1}{ N 6's}
i.e, Hence
√111...1111 {1998 times} = 3333.... 33 {1997 times} (.) 333..333 {998 times} 1 666....666 {1998 times}
Therefore, 1000th digit = 1
1001th digit = 6
4 >
we see 2499 is the last number for which abcd and 4 abcd both are 4 digit
so 1≤a ≤2 , 1≤b≤4 and 1≤c,d≤9
we have
4(1000a + 100b + 10c + d) = (1000d + 100c + 8b ) + 2b + a
If x+y = z , and any two are divisible by d,the rest is also divisible by d
so 4|2b + a or a is even so a = 2
Now 4| 2b + 2 or 2|b + 1 so b is odd
Also we can say that d is either 3 or 8 because 4*3 and 8*4 only gives unit digit as 2
as a = 2 , d ≥8 so d= 8
putting
a= 2 and d=8 in the above equation we get
13b + 1 = 2c
which gives b =1 and c = 7
so the number is 2178
edit : it will be 1≤b≤9 instead of 1≤b≤4
In fact i got that 21978 is such a number that 4abcde = edcba
219978 is such a number that 4 abcdef = fedcba
2199978 is such a number that 4 abcdefg = gfedcba
21999978 is such a number that 4 abcdefgh = hgfedcba
the pattern continues....... isn't it cool ?