21is it any new thing?
does not f = sin satisfy the condition?
If F''(x) + F(x) = 0
F'(0) = 0
F(0) = 0
prove that F(x) = 0 for all real x
-
UP 0 DOWN 0 0 23
23 Answers
21can u please check if the application of taylor expansion was valid here
i applied it without being much aware of it
http://www.targetiit.com/iit-jee-forum/posts/equations-pls-help-18306.html
341sorry, i was not making myself clear. I meant fn(0) = 0.
the given function is infinitely differentiable everywhere. But that does not guarantee that it has a taylor expansion that converges to f everywhere. There are only few examples of such functions (that are known as entire functions in complex analysis)
21# 20
I think taylor expansion can not be used for discontinuous functions,as the proof was given by comparing it to a polynomial and polynomial function is always continuous. is there any other cases where it is not valid?
21sir can u please show how fn(x) = 0
what i can see is fn(0) = 0
so by maclaurine expansion (or putting a =0 in taylor expansion)
f(x) = f(0) + f'(0)x/1! + f''(0) x2/2! +.....
f(x) = 0
341You can google taylor expansion. this is just indicative, this is not a rigorous proof by any means! The taylor expansion may not be valid everywhere.
1@prophet sir,
i din understand what is taylor expansion and how does it help us conclude that f(x)=f(0)=0?
341Also, you can see that the function is infinitely differentiable and for any fn(x) = 0.
That indicates by Taylor expansion f(x) = f(0) = 0.
23f''+f=0
multiply both sides by f' and integrate wrt x
so (f'(x))2 + f(x)2 = 0
so both are zero
23f" + f = 0
integrating both sides from 0 to x
0∫x f dx = - f '(x) [ f'(0) = 0 ]
now consider only the first quadrant ,
and consider an infintesimally small x coordinate = h ,
if we assume f ' (x) to be zero in this small region , then the function is increasing from 0 to h , ad since f(0) = 0 , the graph from 0 to h lies above x axis , and hence area under the graph should be +ve
but we wrote 0∫x f dx = - f '(x)
and we assumed f' > 0 , so 0∫x f dx will come out -ve ,which is contradictory ,
similarly if we assume f'(x) < 0 we again get contradiction
hence f(x) will neither be increasing nor decreasing in first quadrant
similarly we can prove for second quadrant . hence f is neither increasing noe decreasing
hence proved
36F''(x) + F(x) = 0
On putting x = 0 we get, F''(x) = 0
So, F(x) = 0 - F''(x) = 0
and so.... maybe
see i m a student of Xth so i m sorry if there's any mistake and i m not in touch with these problems but only tried.....!!
1i never said tht f"(x) + f(x) = 0 alone says f''(x) = f'(x)
i said f"(x) + f(x) = 0 and f'(x)=[f(x+h)-f(x)]/h together say f"(x)=f'(x)
21i am never saying f is sinx
i am just saying from f"(x) + f(x) = 0
u cant say f''(x) = f'(x)
f = sin only says that if f"(x) + f(x) = 0
u cant say f"(x) = f'(x)
1dude ur counter example itself is wrong f(x) can't be sin x....since d(sin x)/dx≠0 when x=0[1]
1see wat i did was substitute for f(x) by -f"(x) in definition of f'(x)...it gives f"(x)=f'(x)....isn't it?
21proof of the lemma #7
consider G(x) = f(x) - bsinx - a cos x
G''(x) + G(x) = 0 (because f''(x) + f(x) = 0)
G'(0) = 0
G(0) = 0
so G(x) = 0
so f(x) = bsin x + a cos x
21considering f(x) = sin(x+y)
we see f''(x) + f(x) = 0
f(0) = siny
f'(0) = cosy
using above lemma f(x) = sinx cosy + cosx siny
21In fact it can be proved that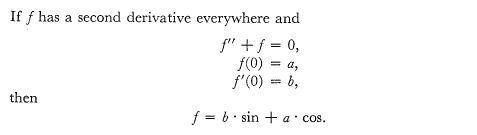 
using it we can give an alternative proof of the identity
sin(x+ y) = sin x cos y + cos x siny
21consider G(x) = [F'(x)]2 + [F(x)]2
G'(x) = 0 so G(x) is constant
G(0) = 0
so G(x) = 0 for all real x
as G(x) = [F'(x)]2 + [F(x)]2
F is zero for all real x
@ kunl how u got F''(x) = F'(x) take F = sin and check
1using F''(x)+F(x)=0 and definition of F(x) we get F"(x)=F'(x)which is ultimately equal to -F(x).
also we are given F'(0)=F"(0)=-F(0)=0
combining this with the result F''(x)=F'(x)=-F(x) the only way this is possible is when F(x)=0 for all real x.
1F''(x)+F(x)=0
Putting x=0
F''(0)+F(0)=0
But given that F(0)=0
So F''(0)=0
Rahulmishra F''(0)=0 butF''(x) need not to be equal to zero.And please check your working also.